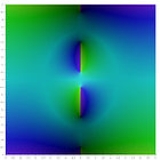
Z function
Encyclopedia
In mathematics
, the Z-function is a function
used for studying the
Riemann zeta-function along the critical line
where the real part of the
argument is one-half.
It is also called the Riemann-Siegel Z-function,
the Riemann-Siegel zeta-function,
the Hardy function,
the Hardy Z-function and
the Hardy zeta-function.
It can be defined in terms of the Riemann-Siegel theta-function and the Riemann zeta-function by
It follows from the functional equation of the Riemann zeta-function that the Z-function is real for real values of t. It is an even function, and real analytic for real values. It follows from the fact that the Riemann-Siegel theta-function and the Riemann zeta-function are both holomorphic in the critical strip, where the imaginary part of t is between -1/2 and 1/2, that the Z-function is holomorphic in the critical strip also. Moreover, the real zeros of Z(t) are precisely the zeros of the zeta-function along the critical line, and complex zeros in the Z-function critical strip correspond to zeros off the critical line of the Riemann zeta-function in its critical strip.
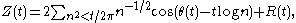
where the error term R(t) has a complex asymptotic expression in terms of the function
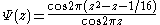
and its derivatives. If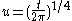
,
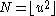and 
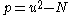then
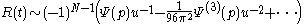
where the ellipsis indicates we may continue on to higher and increasingly complex terms.
Other efficient series for Z(t) are known, in particular several using the
incomplete gamma function
. If
then an especially nice example is
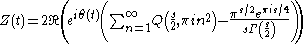
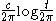
for some constant c > 2/5. Hence, the number of zeros in an interval of a given size slowly increases. If the Riemann hypothesis
is true, all of the zeros in the critical strip are real zeros, and the constant c is one. It is also postulated that all of these zeros are simple zeros.
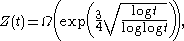
where the notation means that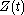
times the function within the Ω does not tend to zero with increasing t.
average from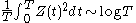
or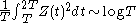
which tell us that the RMS size of Z(t) grows as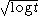
.
This estimate can be improved to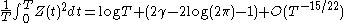
If we increase the exponent, we get an average value which depends more on the peak values of Z. For fourth powers, we have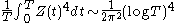
from which we may conclude that the fourth root of the mean fourth power grows as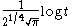
.
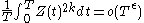
for every positive ε. Here the little "o" notation means that the left hand side divided by the right hand side does converge to zero; in other words little o is the negation of Ω. This conjecture is called the Lindelöf hypothesis, and is weaker than the Riemann hypothesis. It is normally stated in an important equivalent form, which is
in either form it tells us the rate of growth of the peak values cannot be too high. The best known bound on this rate of growth is not strong, telling us that for any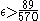
we have that Z(t) is o(tε). It would be astonishing to find that the Z-function grew anywhere close to as fast as this. Littlewood proved that on the Riemann hypothesis,
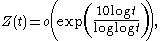
and this seems far more likely.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Z-function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
used for studying the
Riemann zeta-function along the critical line
Critical Line
Critical Line is a contemporary art exhibition center which opened May 5, 2006. It is one of two major projects of the nonprofit art organization ArtRod. Critical Line opened in the St. Helens section of the Theatre District of Downtown Tacoma, Washington...
where the real part of the
argument is one-half.
It is also called the Riemann-Siegel Z-function,
the Riemann-Siegel zeta-function,
the Hardy function,
the Hardy Z-function and
the Hardy zeta-function.
It can be defined in terms of the Riemann-Siegel theta-function and the Riemann zeta-function by
It follows from the functional equation of the Riemann zeta-function that the Z-function is real for real values of t. It is an even function, and real analytic for real values. It follows from the fact that the Riemann-Siegel theta-function and the Riemann zeta-function are both holomorphic in the critical strip, where the imaginary part of t is between -1/2 and 1/2, that the Z-function is holomorphic in the critical strip also. Moreover, the real zeros of Z(t) are precisely the zeros of the zeta-function along the critical line, and complex zeros in the Z-function critical strip correspond to zeros off the critical line of the Riemann zeta-function in its critical strip.
 |
 |
 |
 |
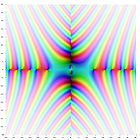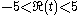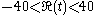The Riemann-Siegel formula
Calculation of the value of Z(t) for real t, and hence of the zeta-function along the critical line, is greatly expedited by the Riemann-Siegel formula. This formula tells us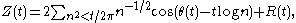where the error term R(t) has a complex asymptotic expression in terms of the function
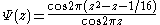
and its derivatives. If
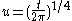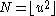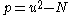, and then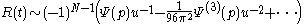where the ellipsis indicates we may continue on to higher and increasingly complex terms.
Other efficient series for Z(t) are known, in particular several using the
incomplete gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
. If
then an especially nice example is
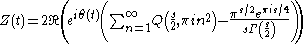
Behavior of the Z-function
From the critical line theorem, it follows that the density of the real zeros of the Z-function is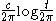for some constant c > 2/5. Hence, the number of zeros in an interval of a given size slowly increases. If the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is true, all of the zeros in the critical strip are real zeros, and the constant c is one. It is also postulated that all of these zeros are simple zeros.
An Omega theorem
Because of the zeros of the Z-function, it exhibits oscillatory behavior. It also slowly grows both on average and in peak value. For instance, we have, even without the Riemann hypothesis, the Omega theorem that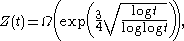where the notation means that
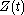times the function within the Ω does not tend to zero with increasing t.Average growth
The average growth of the Z-function has also been much studied. We can find the root mean squareRoot mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
average from
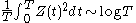
or
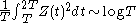
which tell us that the RMS size of Z(t) grows as
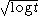.This estimate can be improved to
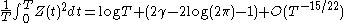
If we increase the exponent, we get an average value which depends more on the peak values of Z. For fourth powers, we have
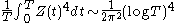
from which we may conclude that the fourth root of the mean fourth power grows as
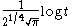.The Lindelöf hypothesis
Higher even powers have been much studied, but less is known about the corresponding average value. It is conjectured, and follows from the Riemann hypothesis, that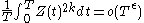for every positive ε. Here the little "o" notation means that the left hand side divided by the right hand side does converge to zero; in other words little o is the negation of Ω. This conjecture is called the Lindelöf hypothesis, and is weaker than the Riemann hypothesis. It is normally stated in an important equivalent form, which is
in either form it tells us the rate of growth of the peak values cannot be too high. The best known bound on this rate of growth is not strong, telling us that for any
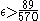we have that Z(t) is o(tε). It would be astonishing to find that the Z-function grew anywhere close to as fast as this. Littlewood proved that on the Riemann hypothesis,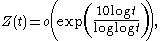and this seems far more likely.