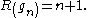Riemann-Siegel theta function
Encyclopedia
In mathematics
, the Riemann–Siegel theta function is defined in terms of the Gamma function
as
for real values of t. Here the argument is chosen in such a way that a continuous function is obtained, i.e., in the same way that the principal branch
of the log Gamma function is defined.
It has an asymptotic expansion
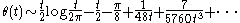
which is not convergent, but whose first few terms give a good approximation for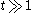
.
It is of interest in studying the Riemann zeta function, since it gives the argument of the zeta function on the critical line
.
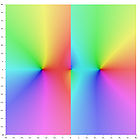
The Riemann–Siegel theta function is an odd real analytic function for real values of t; it is an increasing function for values |t| > 6.29.
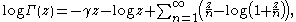
where γ is Euler's constant
. Substituting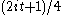
for z and taking the imaginary part termwise gives the following series for θ(t)
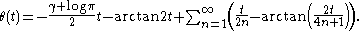
For values with imaginary part between -1 and 1, the arctangent function is holomorphic
, and it is easily seen that the series converges uniformly on compact sets in the region with imaginary part between -1/2 and 1/2, leading to a holomorphic function on this domain. It follows that the Z function
is also holomorphic in this region, which is the critical strip.
We may use the identities
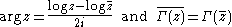
to obtain the closed-form expression
which extends our original definition to a holomorphic function of t. Since the principal branch of log Γ has a single branch cut along the negative real axis, θ(t) in this definition inherits branch cuts along the imaginary axis above i/2 and below -i/2.
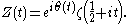
If
is a real number
, then the Z function
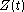returns real values.
Hence the zeta function on the critical line will be real when
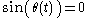. Positive real values of 
where this occurs are called Gram points, after J. P. Gram
, and can of course also be described as the points where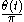
is an integer.
A Gram point is a solution
of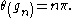
Here are some examples of Gram points
Gram points are useful when computing the zeros of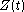
. At a Gram point 
,
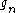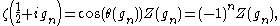
and if this is positive at two successive Gram points,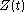
must have a zero in the interval.
According to Gram’s law, the real part is usually positive while the imaginary part alternates with the gram points, between positive and negative values at somewhat regular intervals.
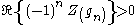
The number of roots,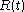
, in the strip from 0 to t, can be found by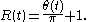
If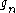
obeys Gram’s law, then finding the number of roots in the strip simply becomes
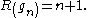
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemann–Siegel theta function is defined in terms of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
as
for real values of t. Here the argument is chosen in such a way that a continuous function is obtained, i.e., in the same way that the principal branch
Principal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
of the log Gamma function is defined.
It has an asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
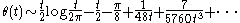
which is not convergent, but whose first few terms give a good approximation for
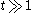.It is of interest in studying the Riemann zeta function, since it gives the argument of the zeta function on the critical line
Critical Line
Critical Line is a contemporary art exhibition center which opened May 5, 2006. It is one of two major projects of the nonprofit art organization ArtRod. Critical Line opened in the St. Helens section of the Theatre District of Downtown Tacoma, Washington...
.The Riemann–Siegel theta function is an odd real analytic function for real values of t; it is an increasing function for values |t| > 6.29.
Theta as a function of a complex variable
We have an infinite series expression for the log Gamma function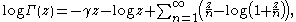where γ is Euler's constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
. Substituting
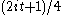for z and taking the imaginary part termwise gives the following series for θ(t)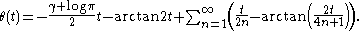For values with imaginary part between -1 and 1, the arctangent function is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, and it is easily seen that the series converges uniformly on compact sets in the region with imaginary part between -1/2 and 1/2, leading to a holomorphic function on this domain. It follows that the Z function
Z function
In mathematics, the Z-function is a function used for studying theRiemann zeta-function along the critical line where the real part of theargument is one-half.It is also called the Riemann-Siegel Z-function,the Riemann-Siegel zeta-function,...
is also holomorphic in this region, which is the critical strip.
We may use the identities
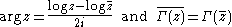
to obtain the closed-form expression
which extends our original definition to a holomorphic function of t. Since the principal branch of log Γ has a single branch cut along the negative real axis, θ(t) in this definition inherits branch cuts along the imaginary axis above i/2 and below -i/2.
 |
 |
 |
 |
 |
 |
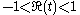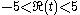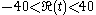Gram points
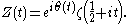
The Riemann zeta function on the critical line can be writtenIf
is a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, then the Z function
Z function
In mathematics, the Z-function is a function used for studying theRiemann zeta-function along the critical line where the real part of theargument is one-half.It is also called the Riemann-Siegel Z-function,the Riemann-Siegel zeta-function,...
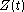returns real values.Hence the zeta function on the critical line will be real when
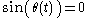. Positive real values of where this occurs are called Gram points, after J. P. GramJørgen Pedersen Gram
Jørgen Pedersen Gram was a Danish actuary and mathematician who was born in Nustrup, Duchy of Schleswig, Denmark and died in Copenhagen, Denmark....
, and can of course also be described as the points where
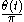is an integer.A Gram point is a solution
of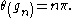Here are some examples of Gram points
 |
 |
|---|---|
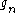| 0 | 17.8455995404 |
| 1 | 23.1702827012 |
| 2 | 27.6701822178 |
Gram points are useful when computing the zeros of
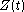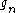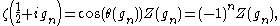
. At a Gram point ,and if this is positive at two successive Gram points,
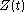must have a zero in the interval.According to Gram’s law, the real part is usually positive while the imaginary part alternates with the gram points, between positive and negative values at somewhat regular intervals.
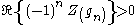
The number of roots,
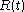, in the strip from 0 to t, can be found by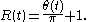If
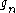obeys Gram’s law, then finding the number of roots in the strip simply becomes