Zarankiewicz problem
Encyclopedia
In the mathematical
field of extremal graph theory
, the Zarankiewicz problem asks how many edges can be added to a bipartite graph
while avoiding a specific bipartite subgraph. Initially, the Polish mathematician Kazimierz Zarankiewicz
proposed the problem of determining the maximum number of edges in an n-vertex graph with no complete bipartite graph
K3,3 as a subgraph, for n ≤ 6; that is, in later notation, he asked for the values of the function Z3(n). The Kővári–Sós–Turán theorem gives a bound on the Zarankiewicz problem when the subgraph to be avoided is a complete bipartite graph.
with a vertices on one side of the bipartition and b vertices on the other side. Define Za,b(m,n) to be the smallest integer k such that every bipartite graph that has m vertices on one side of its bipartition, n vertices on the other side, and k edges contains a subgraph isomorphic
to Ka,b.
An alternative and equivalent definition is that Za,b(m,n) is the smallest integer k such that every (0,1)-matrix of size m × n with k 1's must have a set of a rows and b columns such that the corresponding a×b submatrix is made up only of 1's.
For the specific case when m = n and a = b the shorter notation Za(n) = Za,b(m,n) may also be used.
K2,2, but there exist 6-edge subgraphs of K3,3 with no 4-cycle. One such 6-edge graph is shown below in Figure A. However, because K3,3 only has nine edges in total, its seven-edge subgraphs are formed by removing exactly two of its edges. If the two removed edges meet at a vertex, as in Figure B, the remaining graph contains three different 4-cycles, one of which is shown in the figure. If the two removed edges do not meet, as in Figure C, the remaining graph contains two 4-cycles, one of which is shown.
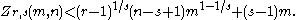
In fact, they proved a similar inequality for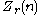
, but shortly afterwards, Hyltén-Cavallius observed that essentially the same argument can be used to prove the above inequality.
For constant r and s with r ≥ s, this bound is O(nm1-(1/s)+m). For r = s = 2 and m = n, this result implies that Z2(n) = O(n3/2); that is, a bipartite graph with 2n vertices and no 4-cycles has O(n3/2) edges, expressed using big O notation
. This bound is within a constant factor of optimal, as the Levi graph
of a finite projective plane
has Θ(n3/2) edges; the absence of 4-cycles in this graph corresponds to the geometric properties that any two lines meet only in a single point and any two points are contained in only a single line of the projective plane. More generally, for r = 2, any s, and m = n, it is known that Z2,s(n,n) = Θ(n3/2) .
Additionally, it is known that Z3(n) = Θ(n5/3) . However, except for some other specific values of r and s, it is not known whether the Kővári–Sós–Turán bound is essentially optimal. Nevertheless, some progress on this question has been made on this question in the last fifty years.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of extremal graph theory
Extremal graph theory
Extremal graph theory is a branch of the mathematical field of graph theory. Extremal graph theory studies extremal graphs which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth...
, the Zarankiewicz problem asks how many edges can be added to a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
while avoiding a specific bipartite subgraph. Initially, the Polish mathematician Kazimierz Zarankiewicz
Kazimierz Zarankiewicz
Kazimierz Zarankiewicz was a Polish mathematician. He was born in Częstochowa and died in London, England.His main interest was topology. He studied at the University of Warsaw, together with Zygmunt Janiszewski, Stefan Mazurkiewicz, Wacław Sierpiński, Kazimierz Kuratowski, and Stanisław Saks...
proposed the problem of determining the maximum number of edges in an n-vertex graph with no complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K3,3 as a subgraph, for n ≤ 6; that is, in later notation, he asked for the values of the function Z3(n). The Kővári–Sós–Turán theorem gives a bound on the Zarankiewicz problem when the subgraph to be avoided is a complete bipartite graph.
Definition
Let Ka,b denote a complete bipartite graphComplete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
with a vertices on one side of the bipartition and b vertices on the other side. Define Za,b(m,n) to be the smallest integer k such that every bipartite graph that has m vertices on one side of its bipartition, n vertices on the other side, and k edges contains a subgraph isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to Ka,b.
An alternative and equivalent definition is that Za,b(m,n) is the smallest integer k such that every (0,1)-matrix of size m × n with k 1's must have a set of a rows and b columns such that the corresponding a×b submatrix is made up only of 1's.
For the specific case when m = n and a = b the shorter notation Za(n) = Za,b(m,n) may also be used.
Example
Z2(3) = 7. That is, every seven-edge subgraph of K3,3 contains a 4-cycleCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
K2,2, but there exist 6-edge subgraphs of K3,3 with no 4-cycle. One such 6-edge graph is shown below in Figure A. However, because K3,3 only has nine edges in total, its seven-edge subgraphs are formed by removing exactly two of its edges. If the two removed edges meet at a vertex, as in Figure B, the remaining graph contains three different 4-cycles, one of which is shown in the figure. If the two removed edges do not meet, as in Figure C, the remaining graph contains two 4-cycles, one of which is shown.
The Kővári–Sós–Turán theorem
The following upper bound was established by Kővári, Sós and Turán shortly after the problem had been posed: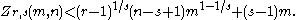In fact, they proved a similar inequality for
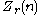, but shortly afterwards, Hyltén-Cavallius observed that essentially the same argument can be used to prove the above inequality.For constant r and s with r ≥ s, this bound is O(nm1-(1/s)+m). For r = s = 2 and m = n, this result implies that Z2(n) = O(n3/2); that is, a bipartite graph with 2n vertices and no 4-cycles has O(n3/2) edges, expressed using big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. This bound is within a constant factor of optimal, as the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of a finite projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
has Θ(n3/2) edges; the absence of 4-cycles in this graph corresponds to the geometric properties that any two lines meet only in a single point and any two points are contained in only a single line of the projective plane. More generally, for r = 2, any s, and m = n, it is known that Z2,s(n,n) = Θ(n3/2) .
Additionally, it is known that Z3(n) = Θ(n5/3) . However, except for some other specific values of r and s, it is not known whether the Kővári–Sós–Turán bound is essentially optimal. Nevertheless, some progress on this question has been made on this question in the last fifty years.