
Extremal graph theory
Encyclopedia
Extremal graph theory is a branch of the mathematical
field of graph theory
. Extremal graph theory studies extremal (maximal or minimal) graphs
which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth. More abstractly, it studies how global properties of a graph influence local substructures of the graph.
For example, a simple extremal graph theory question is "which acyclic graphs on n vertices have the maximum number of edges?" The extremal graphs for this question are trees
on n vertices, which have n − 1 edges. More generally, a typical question is the following. Given a graph property
P, an invariant u, and a set of graphs H, we wish to find the minimum value of m such that every graph in H which has u larger than m possess property P. In the example above, H was the set of n-vertex graphs, P was the property of being cyclic, and u was the number of edges in the graph. Thus every graph on n vertices with more than n − 1 edges must contain a cycle.
Several foundational results in extremal graph theory are questions of the above-mentioned form. For instance, the question of how many edges can an n-vertex graph have before it must contain as subgraph a clique
of size k is answered by Turán's theorem
. Instead of cliques, if the same question is asked for complete multi-partite graphs, the answer is given by the Erdős–Stone theorem
.
determining those graphs of order n, not containing the complete graph Kk of order k, and extremal with respect to size (that is, with as many edges as possible). Another crucial year for the subject was 1975 when Szemerédi proved his result
a vital tool in attacking extremal problems.
. It answers the following question. What is the maximum possible number of edges in an undirected graph G with n vertices which does not contain K3 (three vertices A, B, C with edges AB, AC, BC; i.e. a triangle) as a subgraph? The bipartite graph
where the partite sets differ in their size by at most 1, is the only extremal graph with this property. It contains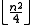
edges. Similar questions have been studied with various other subgraphs H instead of K3; for instance, the Zarankiewicz problem
concerns the largest graph that does not contain a fixed complete bipartite graph
as a subgraph. Turán
also found the (unique) largest graph not containing Kk which is named after him, namely Turán graph
. This graph has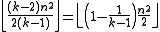
edges. For C4, the largest graph on n vertices not containing C4 has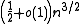
edges.
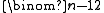
edges to have an isolated vertex - even though almost every possible edge is present in the graph - which means that even a graph with very high density may have no interesting structure covering every vertex. Simple edge counting conditions, which give no indication as to how the edges in the graph are distributed, thus often tend to give uninteresting results for very large structures. Instead, we introduce the concept of minimum degree. The minimum degree of a graph G is defined to be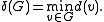
Specifying a large minimum degree removes the objection that there may be a few 'pathological' vertices; if the minimum degree of a graph G is 1, for example, then there can be no isolated vertices (even though G may have very few edges).
A classic result is Dirac's theorem, which states that every graph G with n vertices and minimum degree at least n/2 contains a Hamilton cycle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. Extremal graph theory studies extremal (maximal or minimal) graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth. More abstractly, it studies how global properties of a graph influence local substructures of the graph.
For example, a simple extremal graph theory question is "which acyclic graphs on n vertices have the maximum number of edges?" The extremal graphs for this question are trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
on n vertices, which have n − 1 edges. More generally, a typical question is the following. Given a graph property
Graph property
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...
P, an invariant u, and a set of graphs H, we wish to find the minimum value of m such that every graph in H which has u larger than m possess property P. In the example above, H was the set of n-vertex graphs, P was the property of being cyclic, and u was the number of edges in the graph. Thus every graph on n vertices with more than n − 1 edges must contain a cycle.
Several foundational results in extremal graph theory are questions of the above-mentioned form. For instance, the question of how many edges can an n-vertex graph have before it must contain as subgraph a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
of size k is answered by Turán's theorem
Turán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
. Instead of cliques, if the same question is asked for complete multi-partite graphs, the answer is given by the Erdős–Stone theorem
Erdos–Stone theorem
In extremal graph theory, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem to bound the number of edges in an H-free graph for a non-complete graph H...
.
History
Extremal graph theory started in 1941 when Turán proved his theoremTurán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
determining those graphs of order n, not containing the complete graph Kk of order k, and extremal with respect to size (that is, with as many edges as possible). Another crucial year for the subject was 1975 when Szemerédi proved his result
Szemerédi's theorem
In number theory, Szemerédi's theorem is a result that was formerly the Erdős–Turán conjecture...
a vital tool in attacking extremal problems.
Density results
A typical result in extremal graph theory is Turán's theoremTurán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
. It answers the following question. What is the maximum possible number of edges in an undirected graph G with n vertices which does not contain K3 (three vertices A, B, C with edges AB, AC, BC; i.e. a triangle) as a subgraph? The bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
where the partite sets differ in their size by at most 1, is the only extremal graph with this property. It contains
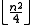
edges. Similar questions have been studied with various other subgraphs H instead of K3; for instance, the Zarankiewicz problem
Zarankiewicz problem
In the mathematical field of extremal graph theory, the Zarankiewicz problem asks how many edges can be added to a bipartite graph while avoiding a specific bipartite subgraph...
concerns the largest graph that does not contain a fixed complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
as a subgraph. Turán
Turan
Tūrān is the Persian name for Central Asia, literally meaning "the land of the Tur". As described below, the original Turanians are an Iranian tribe of the Avestan age. As a people the "Turanian" are one of the two Iranian peoples both descending from the Persian Fereydun but with different...
also found the (unique) largest graph not containing Kk which is named after him, namely Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
. This graph has
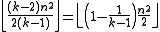
edges. For C4, the largest graph on n vertices not containing C4 has
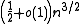
edges.
Minimum degree conditions
The preceding theorems give conditions for a small object to appear within a (perhaps) very large graph. At the opposite extreme, one might search for conditions which force the existence of a structure which covers every vertex. But it is possible for a graph with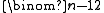
edges to have an isolated vertex - even though almost every possible edge is present in the graph - which means that even a graph with very high density may have no interesting structure covering every vertex. Simple edge counting conditions, which give no indication as to how the edges in the graph are distributed, thus often tend to give uninteresting results for very large structures. Instead, we introduce the concept of minimum degree. The minimum degree of a graph G is defined to be
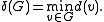
Specifying a large minimum degree removes the objection that there may be a few 'pathological' vertices; if the minimum degree of a graph G is 1, for example, then there can be no isolated vertices (even though G may have very few edges).
A classic result is Dirac's theorem, which states that every graph G with n vertices and minimum degree at least n/2 contains a Hamilton cycle.

