Zig-zag product
Encyclopedia
In graph theory
, the zig-zag product of regular graph
s
, denoted by 
, takes a large graph (
) and a small graph (
), and produces a graph that approximately inherits the size of the large one but the degree of the small one. An important property of the zig-zag product is that if 
is a good expander
, then the expansion of the resulting graph is only slightly worse than the expansion of
.
Roughly speaking, the zig-zag product
replaces each vertex of 
with a copy (cloud) of 
, and connects the vertices by moving a small step (zig) inside a cloud, followed by a big step (zag) between two clouds, and finally performs another small step inside the destination cloud.
The zigzag product was introduced by . When the zig-zag product was first introduced, it was used for the explicit construction of constant degree expanders and extractors. Later on the zig-zag product was used in computational complexity theory
to prove that symmetric logspace
and logspace
are equal .
be a 
-regular graph on 
with rotation map
and let 
be a 
-regular graph on 
with rotation map 
.
The zig-zag product
is defined to be the 
-regular graph on 
whose rotation map 
is as follows:
:
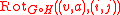to a new graph which is 
-regular. Thus if 
is a significantly larger than 
, the zigzag product will reduce the degree of 
. Roughly speaking, by amplifying each vertex of 
into a cloud of the size of 
the product in fact splits the edges of each original vertex between the vertices of the cloud that replace it.
is a “good enough” expander (has a large spectral gap) then the expansion of the zigzag product is close to to the original expansion of 
.
Formally: Define a
-graph as any 
-regular graph on 
vertices, whose second largest eigenvalue (of the associated random walk) has absolute value at most 
.
Let
be a 
-graph and 
be a 
-graph, then 
is a 
-graph, where 
.
operates separately on each connected component of 
.
Formally speaking, given two graphs:
, a 
-regular graph on 
and 
, a 
-regular graph on 
- if 
is a connected component of 
then 
, where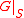 
is the subgraph of 
induced by 
(i.e., the graph on 
which contains all of the edges in 
between vertices in 
).
From the properties of the zigzag product mentioned above, we see that the product of a large graph with a small graph, inherits a size similar to the large graph, and degree similar to the small graph, while preserving its expansion properties from both, thus enabling to increase the size of the expander without deleterious effects.
problem, the problem of testing whether there is a path between two given vertices in an undirected graph, using only logarithmic space. The algorithm relies heavily on the zigzag product.
Roughly speaking, in order to solve the undirected s-t connectivity problem in logarithmic space, the input graph is transformed, using a combination of powering and the zigzag product, into a constant-degree regular graph with a logarithmic diameter. The power product increases the expansion (hence reduces the diameter) in the price of increasing the degree, and the zigzag product is used to reduce the degree while preserving the expansion.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the zig-zag product of regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s
, denoted by , takes a large graph () and a small graph (), and produces a graph that approximately inherits the size of the large one but the degree of the small one. An important property of the zig-zag product is that if is a good expanderExpander graph
In combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...
, then the expansion of the resulting graph is only slightly worse than the expansion of
.Roughly speaking, the zig-zag product
replaces each vertex of with a copy (cloud) of , and connects the vertices by moving a small step (zig) inside a cloud, followed by a big step (zag) between two clouds, and finally performs another small step inside the destination cloud.The zigzag product was introduced by . When the zig-zag product was first introduced, it was used for the explicit construction of constant degree expanders and extractors. Later on the zig-zag product was used in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
to prove that symmetric logspace
SL (complexity)
In computational complexity theory, SL is the complexity class of problems log-space reducible to USTCON , which is the problem of determining whether there exists a path between two vertices in an undirected graph, otherwise described as the problem of determining whether two vertices are in the...
and logspace
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
are equal .
Definition
Let be a -regular graph on with rotation mapRotation map
In mathematics, a rotation map is a function that represents an undirected edge-labeled graph, where each vertex enumerates its outgoing neighbors...
and let be a -regular graph on with rotation map .The zig-zag product
is defined to be the -regular graph on whose rotation map is as follows::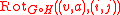
- Let
. - Let
. - Let
. - Output
.
Reduction of the degree
It is immediate from the definition of the zigzag product that it transforms a graph to a new graph which is -regular. Thus if is a significantly larger than , the zigzag product will reduce the degree of . Roughly speaking, by amplifying each vertex of into a cloud of the size of the product in fact splits the edges of each original vertex between the vertices of the cloud that replace it.Spectral gap preservation
The expansion of a graph can be measured by its spectral gap. An important property of the zigzag product is the preservation of the spectral gap. That is, if is a “good enough” expander (has a large spectral gap) then the expansion of the zigzag product is close to to the original expansion of .Formally: Define a
-graph as any -regular graph on vertices, whose second largest eigenvalue (of the associated random walk) has absolute value at most .Let
be a -graph and be a -graph, then is a -graph, where .Connectivity preservation
The zigzag product operates separately on each connected component of .Formally speaking, given two graphs:
, a -regular graph on and , a -regular graph on - if is a connected component of then , where 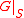is the subgraph of induced by (i.e., the graph on which contains all of the edges in between vertices in ).Construction of constant degree expanders
In 2002 Omer Reingold, Salil Vadhan, and Avi Wigderson have given a simple, explicit combinatorial construction of constant-degree expander graphs. The construction is iterative, and needs as a basic building block a single, expander of constant size. In each iteration the zigzag product is used in order to generate another graph whose size is increased but its degree and expansion remains unchanged. This process continues, yielding arbitrarily large expanders.From the properties of the zigzag product mentioned above, we see that the product of a large graph with a small graph, inherits a size similar to the large graph, and degree similar to the small graph, while preserving its expansion properties from both, thus enabling to increase the size of the expander without deleterious effects.
Solving the undirected s-t connectivity problem in logarithmic space
In 2005 Omer Reingold introduced an algorithm that solves the undirected st-connectivityST-connectivity
In computer science and computational complexity theory, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.Formally, the decision problem is given by- Complexity :...
problem, the problem of testing whether there is a path between two given vertices in an undirected graph, using only logarithmic space. The algorithm relies heavily on the zigzag product.
Roughly speaking, in order to solve the undirected s-t connectivity problem in logarithmic space, the input graph is transformed, using a combination of powering and the zigzag product, into a constant-degree regular graph with a logarithmic diameter. The power product increases the expansion (hence reduces the diameter) in the price of increasing the degree, and the zigzag product is used to reduce the degree while preserving the expansion.