
ATLAS of Finite Groups
Encyclopedia
The ATLAS of Finite Groups, often simply known as the ATLAS, is a group theory
book by John Horton Conway
, Robert Turner Curtis, Simon Phillips Norton
, Richard Alan Parker
and Robert Arnott Wilson
(with computational assistance from J. G. Thackray), published in December 1985 by Oxford University Press
and reprinted with corrections in 2003 (ISBN 978-0-19-853199-9). It lists basic information about 93 finite simple
groups, the information being generally: its order, Schur multiplier
, outer automorphism group
, various constructions (such as presentations
), conjugacy classes of maximal subgroup
s (with characters group action
they define), and, most importantly, character table
s (including power maps on the conjugacy classes) of the group itself and bicyclic extensions given by stem extensions and automorphism groups. In certain cases (such as for the Chevalley groups
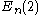 ), the character table is not listed and only basic information is given.
), the character table is not listed and only basic information is given.
The ATLAS is a recognizable large format book (sized 420mm by 300mm) with a cherry red cardboard cover and spiral binding. The names of the authors, all six letters long, are printed on the cover in the form of an array which evokes the idea of a character table.
The ATLAS is being continued in the form of an electronic database, the ATLAS of Finite Group Representations.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
book by John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, Robert Turner Curtis, Simon Phillips Norton
Simon P. Norton
Simon Phillips Norton is a mathematician in Cambridge, England, who works on finite simple groups. He constructed the Harada–Norton group, and in 1979 together with John Conway proved there is a connection between the Monster group and the j-function in number theory. They dubbed this monstrous...
, Richard Alan Parker
Richard A. Parker
Richard A. Parker is a mathematician and freelance computer programmer in Cambridge, England. He invented many of the algorithms for computing the modular character tables of finite simple groups...
and Robert Arnott Wilson
Robert Arnott Wilson
Robert Arnott Wilson is a mathematician in London, England, who is best known for his work on classifying the maximal subgroups of finite simple groups and for the work in the Monster group.-Books:...
(with computational assistance from J. G. Thackray), published in December 1985 by Oxford University Press
Oxford University Press
Oxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
and reprinted with corrections in 2003 (ISBN 978-0-19-853199-9). It lists basic information about 93 finite simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
groups, the information being generally: its order, Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
, outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
, various constructions (such as presentations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
), conjugacy classes of maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
s (with characters group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
they define), and, most importantly, character table
Character table
In group theory, a character table is a two-dimensional table whose rows correspond to irreducible group representations, and whose columns correspond to classes of group elements...
s (including power maps on the conjugacy classes) of the group itself and bicyclic extensions given by stem extensions and automorphism groups. In certain cases (such as for the Chevalley groups
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
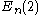 ), the character table is not listed and only basic information is given.
), the character table is not listed and only basic information is given.The ATLAS is a recognizable large format book (sized 420mm by 300mm) with a cherry red cardboard cover and spiral binding. The names of the authors, all six letters long, are printed on the cover in the form of an array which evokes the idea of a character table.
The ATLAS is being continued in the form of an electronic database, the ATLAS of Finite Group Representations.

