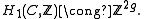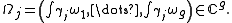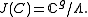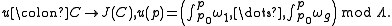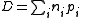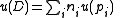Abel–Jacobi map
Encyclopedia
In mathematics
, the Abel–Jacobi map is a construction of algebraic geometry
which relates an algebraic curve
to its Jacobian variety
. In Riemannian geometry
, it is a more general construction mapping a manifold
to its Jacobi torus.
The name derives from the theorem of Abel
and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.
Geometrically, this homology group consists of (homology classes of) cycles in C, or in other words, closed loops. Therefore we can choose 2g loops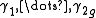
generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
By definition, this is the space of globally defined differential form
s on C, so we can choose g linearly independent forms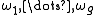
. Given forms and closed loops we can integrate, and we define 2g vectors
It follows from the Riemann bilinear relations that the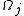
generate a nondegenerate lattice
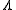(that is, they are a real basis for 
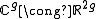), and the Jacobian is defined by
The Abel–Jacobi map is then defined as follows. We pick some base point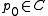
and, nearly mimicking the definition of 
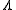, define the map
Although this is seemingly dependent on a path from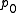
to 
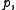any two such paths define a closed loop in 
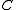and, therefore, an element of 
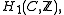so integration over it gives an element of 
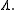Thus the difference is erased in the passage to the quotient by 
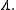. Changing base-point 
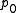does change the map, but only by a translation of the torus.
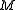be a smooth compact manifold
. Let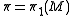
be its fundamental group. Let 
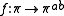be its abelianisation map. Let
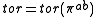be the torsion subgroup of
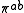. Let 
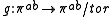
be the quotient by torsion. If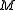
is a surface, 
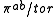is non-canonically isomorphic to
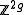, where 
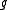is the genus; more generally, 
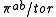is non-canonically isomorphic to 
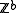, where 
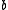is the first Betti number. Let 
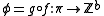be the composite homomorphism.
Definition. The cover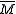
of the manifold
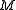corresponding the subgroup 
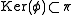is called the universal (or maximal) free abelian
cover.
Now assume M has a Riemannian metric. Let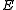
be the space of harmonic 
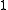-forms on
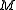, with dual 
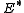canonically identified with
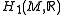. By integrating an integral
harmonic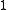
-form along paths from a basepoint 
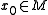, we obtain a map to the circle
.
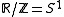Similarly, in order to define a map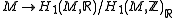
without choosing a basis for
cohomology, we argue as follows. Let
be a point in the
universal cover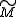
of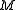 
. Thus
is represented by a point of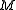 
together
with a path
from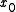 
to it. By
integrating along the path
, we obtain a linear form,
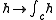, on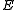 
. We thus obtain a map
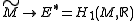, which,
furthermore, descends to a map
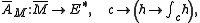
where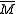
is the universal free abelian cover.
Definition. The Jacobi variety (Jacobi torus) of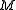
is the
torus
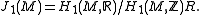
Definition. The Abel–Jacobi map
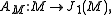
is obtained from the map above by passing to quotients.
The Abel–Jacobi map is unique up to translations of the Jacobi torus. The map has applications in Systolic geometry.
is a divisor (meaning a formal integer-linear combination of points of C). We can define
and therefore speak of the value of the Abel–Jacobi map on divisors. The theorem is then that if D and E are two effective divisors, meaning that the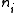
are all positive integers, then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Abel–Jacobi map is a construction of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
which relates an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
to its Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
. In Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, it is a more general construction mapping a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to its Jacobi torus.
The name derives from the theorem of Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.
Construction of the map
In complex algebraic geometry, the Jacobian of a curve C is constructed using path integration. Namely, suppose C has genus g, which means topologically that
Geometrically, this homology group consists of (homology classes of) cycles in C, or in other words, closed loops. Therefore we can choose 2g loops
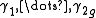generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
-
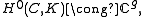where K is the canonical bundleCanonical bundleIn mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
on C.
By definition, this is the space of globally defined differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on C, so we can choose g linearly independent forms
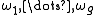. Given forms and closed loops we can integrate, and we define 2g vectors
It follows from the Riemann bilinear relations that the
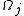generate a nondegenerate latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
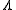(that is, they are a real basis for 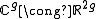), and the Jacobian is defined by
The Abel–Jacobi map is then defined as follows. We pick some base point
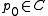and, nearly mimicking the definition of 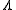, define the map
Although this is seemingly dependent on a path from
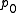to 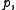any two such paths define a closed loop in 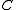and, therefore, an element of 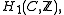so integration over it gives an element of 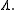Thus the difference is erased in the passage to the quotient by 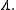. Changing base-point 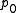does change the map, but only by a translation of the torus.Invariant construction of the Abel–Jacobi map
Let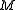 be a smooth compact manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Let
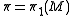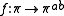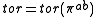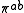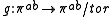
be its fundamental group. Let be its abelianisation map. Let be the torsion subgroup of. Let be the quotient by torsion. If
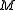is a surface, 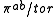is non-canonically isomorphic to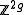, where 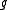is the genus; more generally, 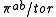is non-canonically isomorphic to 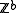, where 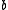is the first Betti number. Let 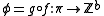be the composite homomorphism.Definition. The cover
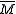of the manifold 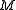corresponding the subgroup 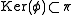is called the universal (or maximal) free abeliancover.
Now assume M has a Riemannian metric. Let
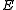be the space of harmonic 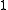-forms on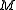, with dual 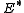canonically identified with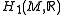. By integrating an integralharmonic
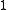-form along paths from a basepoint 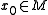, we obtain a map to the circle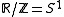.Similarly, in order to define a map
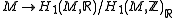without choosing a basis forcohomology, we argue as follows. Let
be a point in theuniversal cover
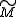of 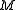. Thus is represented by a point of 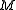togetherwith a path
from 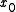to it. Byintegrating along the path
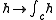, we obtain a linear form,, on 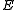. We thus obtain a map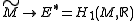, which,furthermore, descends to a map
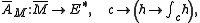
where
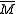is the universal free abelian cover.Definition. The Jacobi variety (Jacobi torus) of
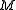is thetorus
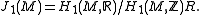
Definition. The Abel–Jacobi map
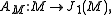
is obtained from the map above by passing to quotients.
The Abel–Jacobi map is unique up to translations of the Jacobi torus. The map has applications in Systolic geometry.
Abel–Jacobi theorem
The following theorem was proved by Abel and Jacobi (each one proved one implication): Suppose that
is a divisor (meaning a formal integer-linear combination of points of C). We can define
and therefore speak of the value of the Abel–Jacobi map on divisors. The theorem is then that if D and E are two effective divisors, meaning that the
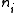are all positive integers, then
-
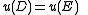if and only if 
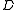is linearly equivalent to 
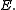This implies that the Abel–Jacobi map induces an isomorphism (of abelian groups) between the space of divisor classes of degree zero and the Jacobian.