Abouabdillah's theorem
Encyclopedia
Abouabdillah's theorem refers to two distinct theorem
s in mathematics
, proven by Moroccan mathematician Driss Abouabdillah: one in geometry
and one in number theory
.
preserve circles and spheres. Conversely, Abouabdillah's theorem states that every injective or surjective transformation of a Euclidean space that preserves circles or spheres is a similarity
.
More precisely:
Theorem. Let
be a Euclidean affine space
of dimension at least 2. Then:
1. Every surjective mapping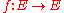
that transforms any four concyclic points
into four concyclic points is a similarity.
2. Every injective mapping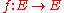
that transforms any circle into a circle is a similarity.
s in the partially ordered set
EN consisting of the positive integers in the interval [1,N], partially ordered by divisibility. With this partial order, an antichain is a set of integers within this interval, such that no member of this set is a divisor of any other member. It possible to prove using ideas related to Dilworth's theorem
that the maximum number of elements in an antichain of E2n is exactly n: there exists an antichain of this size consisting of all the numbers in the subinterval [n + 1,2n], so the maximum size of an antichain is at least n. However, there are only n odd numbers within the interval [1,2n], for each odd number c in this interval at most one number of the form 2kc may belong to any antichain, and every number in the interval has this form for some c, so the maximum size of an antichain is also at most n.
Abouabdillah's theorem characterizes more precisely the numbers that may belong to an antichain of maximum size in E2n. Specifically, if x is any integer in the interval [1,2n], decompose x as the product of a power of two
and an odd number: x = 2kc, where c is odd. Then, according to Abouabdillah's theorem, there exists an antichain of cardinality n in E2n that contains x if and only if 2n < 3k + 1c.
The smallest value in any maximum antichain of E2n is at least 2k, where 3k + 1 is the first power of three that is greater than 2n, as had been posed as a problem by and solved by . Lehmer's solution immediately implies the special case of Abouabdillah's theorem for c = 1. Abouabdillah's theorem generalizes this solution to all values within the given interval.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, proven by Moroccan mathematician Driss Abouabdillah: one in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and one in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Geometry
In geometry, similarities of an Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
preserve circles and spheres. Conversely, Abouabdillah's theorem states that every injective or surjective transformation of a Euclidean space that preserves circles or spheres is a similarity
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.
More precisely:
Theorem. Let
be a Euclidean affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
of dimension at least 2. Then:
1. Every surjective mapping
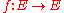that transforms any four concyclic pointsConcyclic points
In geometry, a set of points is said to be concyclic if they lie on a common circle.A circle can be drawn around any triangle. A quadrilateral that can be inscribed inside a circle is said to be a cyclic quadrilateral....
into four concyclic points is a similarity.
2. Every injective mapping
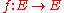that transforms any circle into a circle is a similarity.Number theory
The number-theoretic theorem of Abouabdillah is about antichainAntichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
s in the partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
EN consisting of the positive integers in the interval [1,N], partially ordered by divisibility. With this partial order, an antichain is a set of integers within this interval, such that no member of this set is a divisor of any other member. It possible to prove using ideas related to Dilworth's theorem
Dilworth's theorem
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains...
that the maximum number of elements in an antichain of E2n is exactly n: there exists an antichain of this size consisting of all the numbers in the subinterval [n + 1,2n], so the maximum size of an antichain is at least n. However, there are only n odd numbers within the interval [1,2n], for each odd number c in this interval at most one number of the form 2kc may belong to any antichain, and every number in the interval has this form for some c, so the maximum size of an antichain is also at most n.
Abouabdillah's theorem characterizes more precisely the numbers that may belong to an antichain of maximum size in E2n. Specifically, if x is any integer in the interval [1,2n], decompose x as the product of a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
and an odd number: x = 2kc, where c is odd. Then, according to Abouabdillah's theorem, there exists an antichain of cardinality n in E2n that contains x if and only if 2n < 3k + 1c.
The smallest value in any maximum antichain of E2n is at least 2k, where 3k + 1 is the first power of three that is greater than 2n, as had been posed as a problem by and solved by . Lehmer's solution immediately implies the special case of Abouabdillah's theorem for c = 1. Abouabdillah's theorem generalizes this solution to all values within the given interval.