
Additively indecomposable ordinal
Encyclopedia
In set theory
, a branch of mathematics
, an additively indecomposable ordinal α is any ordinal number
that is not 0 such that for any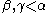 , we have
, we have 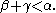 The set of additively indecomposable ordinals is denoted
The set of additively indecomposable ordinals is denoted 
From the continuity of addition in its right argument, we get that if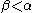 and α is additively indecomposable, then
and α is additively indecomposable, then 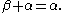
Obviously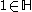 , since
, since 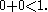 No finite ordinal other than
No finite ordinal other than 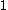 is in
is in  Also,
Also, 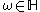 , since the sum of two finite ordinals is still finite. More generally, every infinite cardinal
, since the sum of two finite ordinals is still finite. More generally, every infinite cardinal
is in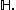
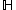 is closed and unbounded, so the enumerating function of
is closed and unbounded, so the enumerating function of 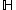 is normal. In fact,
is normal. In fact, 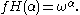
The derivative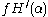 (which enumerates fixed points of fH) is written
(which enumerates fixed points of fH) is written 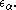 Ordinals of this form (that is, fixed point
Ordinals of this form (that is, fixed point
s of ) are called epsilon numbers
) are called epsilon numbers
. The number is therefore the first fixed point of the sequence
is therefore the first fixed point of the sequence
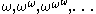
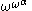 for any ordinal α.
for any ordinal α.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an additively indecomposable ordinal α is any ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
that is not 0 such that for any
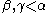 , we have
, we have 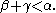 The set of additively indecomposable ordinals is denoted
The set of additively indecomposable ordinals is denoted 
From the continuity of addition in its right argument, we get that if
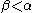 and α is additively indecomposable, then
and α is additively indecomposable, then 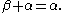
Obviously
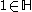 , since
, since 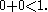 No finite ordinal other than
No finite ordinal other than 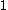 is in
is in 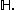 Also,
Also, 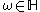 , since the sum of two finite ordinals is still finite. More generally, every infinite cardinal
, since the sum of two finite ordinals is still finite. More generally, every infinite cardinalCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
is in
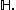
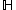 is closed and unbounded, so the enumerating function of
is closed and unbounded, so the enumerating function of 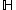 is normal. In fact,
is normal. In fact, 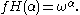
The derivative
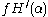 (which enumerates fixed points of fH) is written
(which enumerates fixed points of fH) is written 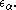 Ordinals of this form (that is, fixed point
Ordinals of this form (that is, fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of
 ) are called epsilon numbers
) are called epsilon numbersEpsilon nought
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like...
. The number
 is therefore the first fixed point of the sequence
is therefore the first fixed point of the sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
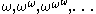
Multiplicatively indecomposable
A similar notion can be defined for multiplication. The multiplicatively indecomposable ordinals are those of the form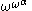 for any ordinal α.
for any ordinal α.See also
- Ordinal arithmeticOrdinal arithmeticIn the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...

