Aeroacoustics
Encyclopedia
Aeroacoustics is a branch of acoustics
that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. Although no complete scientific theory of the generation of noise by aerodynamic flows has been established, most practical aeroacoustic analysis relies upon the so-called Acoustic Analogy
, whereby the governing equations of motion of the fluid are coerced into a form reminiscent of the wave equation
of "classical" (i.e. linear) acoustics.
The most common approach of accomplishing this is through Lighthill's aeroacoustic analogy. It was proposed by James Lighthill
in the 1950s when noise generation associated with the jet engine
was beginning to be placed under scientific scrutiny. Computational Aeroacoustics
(CAA) is the application of numerical methods and computers to find approximate solutions of the governing equations for specific (and likely complicated) aeroacoustic problems.
in
1650. Historically, Aeolus
was the Greek ruler of the winds, and
the Ancient Greeks believed these sounds were the voice of Aeolus. An Aeolian tone is produced when air passes over an obstacle, resulting in trailing vortices that display an oscillatory behavior. These eddies can have strong periodic components, resulting in a steady tone.
For air moving over a cylinder, empirical data shows that an Aeolian tone will be produced with the frequency
where v is the air velocity, d is the diameter of the cylinder, and α is the Strouhal number
, which has a value of about 0.2.
Aeolian sounds can be produced in the rigging of a sail-powered ship. The vortex trails produced as the wind passes over a rope produce a sound with a frequency that varies with the velocity of the wind and the thickness of the rope. Each doubling of the wind velocity results in an octave increase in the tone, allowing up to a six octave variation in a strong, gusty wind. Ships may also carry Helmholtz resonators that amplify these sounds, and the sounds can also be heard among the openings in limestone cliffs. Some songs have been written to emulate these varying wind sounds, such as "The Winter Wind
" by Frédéric Chopin
or "Tempest
" by Ludwig van Beethoven
.
of a compressible viscous fluid
, into an inhomogeneous wave equation
, thereby making a connection between fluid mechanics
and acoustics
. This is often called "Lighthill's analogy" because it presents a model for the acoustic field that is not, strictly speaking, based on the physics of flow-induced/generated noise, but rather on the analogy of how they might be represented through the governing equations of a compressible fluid.
The first equation of interest is the conservation of mass
equation, which reads
where
and 
represent the density and velocity of the fluid, which depend on space and time, and 
is the substantial derivative.
Next is the conservation of momentum equation, which is given by
where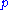
is the thermodynamic pressure
, and
is the viscous (or traceless) part of the stress tensor.
Now, multiplying the conservation of mass equation by
and adding it to the conservation of momentum equation gives
Note that
is a tensor
(see also tensor product
). Differentiating the conservation of mass equation with respect to time, taking the divergence
of the conservation of momentum equation and subtracting the latter from the former, we arrive at
Subtracting
, where 
is the speed of sound
in the medium in its equilibrium (or quiescent) state, from both sides of the last equation and rearranging it results in
which is equivalent to
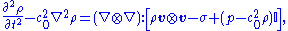
where
is the identity
tensor, and
denotes the (double) tensor contraction
operator.
The above equation is the celebrated Lighthill equation of aeroacoustics. It is a wave equation
with a source term on the right-hand side, i.e. an inhomogeneous wave equation. The argument of the "double-divergence operator" on the right-hand side of last equation, i.e.
, is the so-called Lighthill turbulence stress tensor for the acoustic field, and it is commonly denoted by 
.
Using Einstein notation
, Lighthill’s equation can be written as
where
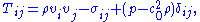
and
is the Kronecker delta. Each of the acoustic source terms, i.e. terms in 
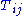, may play a significant role in the generation of noise depending upon flow conditions considered. 
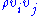describes unsteady convection of flow (or Reynold's Stress), 
describes sound generated by shear, and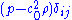 
describes non-linear acoustic generation processes.
In practice, it is customary to neglect the effects of viscosity
on the fluid, i.e. one takes
, because it is generally accepted that the effects of the latter on noise generation, in most situations, are orders of magnitude smaller than those due to the other terms. Lighthill provides an in-depth discussion of this matter.
In aeroacoustic studies, both theoretical and computational efforts are made to solve for the acoustic source terms in Lighthill's equation in order to make statements regarding the relevant aerodynamic noise generation mechanisms present.
Finally, it is important to realize that Lighthill's equation is exact in the sense that no approximations of any kind have been made in its derivation.
, Landau and Lifshitz derive an aeroacoustic equation analogous to Lighthill's (i.e., an equation for sound generated by "turbulent" fluid motion) but for the incompressible flow
of an inviscid fluid. The inhomogeneous wave equation that they obtain is for the pressure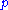
rather than for the density 
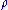of the fluid. Furthermore, unlike Lighthill's equation, Landau and Lifshitz's equation is not exact; it is an approximation.
If one is to allow for approximations to be made, a simpler way (without necessarily assuming the fluid is incompressible) to obtain an approximation to Lighthill's equation is to assume that
, where 
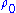and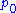 
are the (characteristic) density and pressure of the fluid in its equilibrium state. Then, upon substitution the assumed relation between pressure and density into 
we obtain the equation
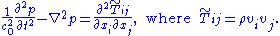
And for the case when the fluid is indeed incompressible, i.e.
(for some positive constant 
) everywhere, then we obtain exactly the equation given in Landau and Lifshitz , namely
A similar approximation [in the context of equation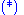
], namely 
, is suggested by Lighthill [see Eq. (7) in the latter paper].
Of course, one might wonder whether we are justified in assuming that
. The answer is in affirmative, if the flow satisfies certain basic assumptions. In particular, if 
and 
, then the assumed relation follows directly from the linear theory of sound waves (see, e.g., the linearized Euler equations and the acoustic wave equation
). In fact, the approximate relation between
and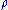 
that we assumed is just a linear approximation
to the generic barotropic
equation of state
of the fluid.
However, even after the above deliberations, it is still not clear whether one is justified in using an inherently linear relation to simplify a nonlinear wave equation. Nevertheless, it is a very common practice in nonlinear acoustics
as the textbooks on the subject show: e.g., Naugolnykh and Ostrovsky and Hamilton and Morfey.
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. Although no complete scientific theory of the generation of noise by aerodynamic flows has been established, most practical aeroacoustic analysis relies upon the so-called Acoustic Analogy
Acoustic analogy
Acoustic analogies are applied mostly in numerical aeroacoustics to reduce aeroacoustic sound sources to simple emitter types. They are therefore often also referred to as aeroacoustic analogies....
, whereby the governing equations of motion of the fluid are coerced into a form reminiscent of the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
of "classical" (i.e. linear) acoustics.
The most common approach of accomplishing this is through Lighthill's aeroacoustic analogy. It was proposed by James Lighthill
James Lighthill
Sir Michael James Lighthill, FRS was a British applied mathematician, known for his pioneering work in the field of aeroacoustics.-Biography:...
in the 1950s when noise generation associated with the jet engine
Jet engine
A jet engine is a reaction engine that discharges a fast moving jet to generate thrust by jet propulsion and in accordance with Newton's laws of motion. This broad definition of jet engines includes turbojets, turbofans, rockets, ramjets, pulse jets...
was beginning to be placed under scientific scrutiny. Computational Aeroacoustics
Computational Aeroacoustics
While the discipline of Aeroacoustics is definitely dated back to the first publication of Sir James Lighthill in the early 1950s, the origin of Computational Aeroacoustics can only very likely be dated back to the middle of the 1980s...
(CAA) is the application of numerical methods and computers to find approximate solutions of the governing equations for specific (and likely complicated) aeroacoustic problems.
Aeolian sound
An Aeolian sound is a sound that is produced by the winds when it passes over naturally occurring objects. They were first remarked upon in published form by Athanasius KircherAthanasius Kircher
Athanasius Kircher was a 17th century German Jesuit scholar who published around 40 works, most notably in the fields of oriental studies, geology, and medicine...
in
1650. Historically, Aeolus
Aeolus
Aeolus was the ruler of the winds in Greek mythology. In fact this name was shared by three mythic characters. These three personages are often difficult to tell apart, and even the ancient mythographers appear to have been perplexed about which Aeolus was which...
was the Greek ruler of the winds, and
the Ancient Greeks believed these sounds were the voice of Aeolus. An Aeolian tone is produced when air passes over an obstacle, resulting in trailing vortices that display an oscillatory behavior. These eddies can have strong periodic components, resulting in a steady tone.
For air moving over a cylinder, empirical data shows that an Aeolian tone will be produced with the frequency
-
,
where v is the air velocity, d is the diameter of the cylinder, and α is the Strouhal number
Strouhal number
In dimensional analysis, the Strouhal number is a dimensionless number describing oscillating flow mechanisms. The parameter is named after Vincenc Strouhal, a Czech physicist who experimented in 1878 with wires experiencing vortex shedding and singing in the wind...
, which has a value of about 0.2.
Aeolian sounds can be produced in the rigging of a sail-powered ship. The vortex trails produced as the wind passes over a rope produce a sound with a frequency that varies with the velocity of the wind and the thickness of the rope. Each doubling of the wind velocity results in an octave increase in the tone, allowing up to a six octave variation in a strong, gusty wind. Ships may also carry Helmholtz resonators that amplify these sounds, and the sounds can also be heard among the openings in limestone cliffs. Some songs have been written to emulate these varying wind sounds, such as "The Winter Wind
Étude Op. 25, No. 11 (Chopin)
Étude Op. 25, No. 11, in A minor, is a solo piano technical study composed by Frédéric Chopin in 1836. It was first published together with all études of Opus 25 in 1837, in France, Germany, and England. The first French edition indicates a common time time signature, but the manuscript and the...
" by Frédéric Chopin
Frédéric Chopin
Frédéric François Chopin was a Polish composer and virtuoso pianist. He is considered one of the great masters of Romantic music and has been called "the poet of the piano"....
or "Tempest
Piano Sonata No. 17 (Beethoven)
The Piano Sonata No. 17 in D minor, Op. 31, No. 2, was composed in 1801/02 by Ludwig van Beethoven. It is usually referred to as "The Tempest" , but this title was not given by him, or indeed referred to as such during his lifetime; instead, it comes from a claim by his associate Anton Schindler...
" by Ludwig van Beethoven
Ludwig van Beethoven
Ludwig van Beethoven was a German composer and pianist. A crucial figure in the transition between the Classical and Romantic eras in Western art music, he remains one of the most famous and influential composers of all time.Born in Bonn, then the capital of the Electorate of Cologne and part of...
.
Lighthill's equation
Lighthill rearranged the Navier–Stokes equations, which govern the flowFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
of a compressible viscous fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
, into an inhomogeneous wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, thereby making a connection between fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
and acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
. This is often called "Lighthill's analogy" because it presents a model for the acoustic field that is not, strictly speaking, based on the physics of flow-induced/generated noise, but rather on the analogy of how they might be represented through the governing equations of a compressible fluid.
The first equation of interest is the conservation of mass
Conservation of mass
The law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
equation, which reads
where
and represent the density and velocity of the fluid, which depend on space and time, and is the substantial derivative.Next is the conservation of momentum equation, which is given by
where
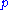is the thermodynamic pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, and
is the viscous (or traceless) part of the stress tensor.Now, multiplying the conservation of mass equation by
and adding it to the conservation of momentum equation givesNote that
is a tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
(see also tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
). Differentiating the conservation of mass equation with respect to time, taking the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the conservation of momentum equation and subtracting the latter from the former, we arrive at
Subtracting
, where is the speed of soundSpeed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
in the medium in its equilibrium (or quiescent) state, from both sides of the last equation and rearranging it results in
which is equivalent to
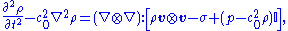
where
is the identityIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
tensor, and
denotes the (double) tensor contractionTensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
operator.
The above equation is the celebrated Lighthill equation of aeroacoustics. It is a wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
with a source term on the right-hand side, i.e. an inhomogeneous wave equation. The argument of the "double-divergence operator" on the right-hand side of last equation, i.e.
, is the so-called Lighthill turbulence stress tensor for the acoustic field, and it is commonly denoted by .Using Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, Lighthill’s equation can be written as
where
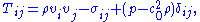
and
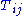is the Kronecker delta. Each of the acoustic source terms, i.e. terms in , may play a significant role in the generation of noise depending upon flow conditions considered. 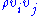describes unsteady convection of flow (or Reynold's Stress), describes sound generated by shear, and 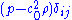describes non-linear acoustic generation processes.In practice, it is customary to neglect the effects of viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
on the fluid, i.e. one takes
, because it is generally accepted that the effects of the latter on noise generation, in most situations, are orders of magnitude smaller than those due to the other terms. Lighthill provides an in-depth discussion of this matter.In aeroacoustic studies, both theoretical and computational efforts are made to solve for the acoustic source terms in Lighthill's equation in order to make statements regarding the relevant aerodynamic noise generation mechanisms present.
Finally, it is important to realize that Lighthill's equation is exact in the sense that no approximations of any kind have been made in its derivation.
Related model equations
In their classical text on fluid mechanicsFluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, Landau and Lifshitz derive an aeroacoustic equation analogous to Lighthill's (i.e., an equation for sound generated by "turbulent" fluid motion) but for the incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
of an inviscid fluid. The inhomogeneous wave equation that they obtain is for the pressure
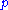rather than for the density 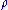of the fluid. Furthermore, unlike Lighthill's equation, Landau and Lifshitz's equation is not exact; it is an approximation.If one is to allow for approximations to be made, a simpler way (without necessarily assuming the fluid is incompressible) to obtain an approximation to Lighthill's equation is to assume that
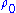, where and 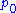are the (characteristic) density and pressure of the fluid in its equilibrium state. Then, upon substitution the assumed relation between pressure and density into we obtain the equation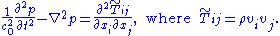And for the case when the fluid is indeed incompressible, i.e.
(for some positive constant ) everywhere, then we obtain exactly the equation given in Landau and Lifshitz , namelyA similar approximation [in the context of equation
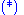], namely , is suggested by Lighthill [see Eq. (7) in the latter paper].Of course, one might wonder whether we are justified in assuming that
. The answer is in affirmative, if the flow satisfies certain basic assumptions. In particular, if and , then the assumed relation follows directly from the linear theory of sound waves (see, e.g., the linearized Euler equations and the acoustic wave equationAcoustic wave equation
In physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
). In fact, the approximate relation between
and 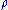that we assumed is just a linear approximationLinear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to the generic barotropic
Barotropic
In meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...
equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
of the fluid.
However, even after the above deliberations, it is still not clear whether one is justified in using an inherently linear relation to simplify a nonlinear wave equation. Nevertheless, it is a very common practice in nonlinear acoustics
Nonlinear acoustics
Non-linear acoustics is a branch of physics dealing with sound waves being distorted as they travel.-Introduction:A sound wave propagates through a material as a localized pressure change...
as the textbooks on the subject show: e.g., Naugolnykh and Ostrovsky and Hamilton and Morfey.
External links
- M. J. Lighthill, "On Sound Generated Aerodynamically. I. General Theory," Proc. R. Soc. Lond. A 211 (1952) pp. 564–587. This article on JSTOR.
- M. J. Lighthill, "On Sound Generated Aerodynamically. II. Turbulence as a Source of Sound," Proc. R. Soc. Lond. A 222 (1954) pp. 1–32. This article on JSTOR.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics 2ed., Course of Theoretical Physics vol. 6, Butterworth-Heinemann (1987) §75. ISBN 0-7506-2767-0, Preview from Amazon.
- K. Naugolnykh and L. Ostrovsky, Nonlinear Wave Processes in Acoustics, Cambridge Texts in Applied Mathematics vol. 9, Cambridge University Press (1998) chap. 1. ISBN 0-521-39984-X, Preview from Google.
- M. F. Hamilton and C. L. Morfey, "Model Equations," Nonlinear Acoustics, eds. M. F. Hamilton and D. T. Blackstock, Academic Press (1998) chap. 3. ISBN 0-12-321860-8, Preview from Google.
- Aeroacoustics at the University of Mississippi
- Aeroacoustics at the University of Leuven
- International Journal of Aeroacoustics
- Examples in Aeroacoustics from NASA
- Aeroacoustics.info