Affine Grassmannian (manifold)
Encyclopedia
In mathematics
, there are two distinct meanings of the term affine Grassmannian. In one it is the manifold of all k-dimensional affine subspaces
of Rn (described on this page), while in the other the affine Grassmannian
is a quotient of a group-ring based on formal Laurent series.
V and a non-negative integer k, then Graffk(V) is the topological space
of all affine
k-dimensional subspaces of V.
It has a natural projection p:Graffk(V) → Grk(V), the Grassmannian
of all linear k-dimensional subspaces of V by defining p(U) to be the translation of U to a subspace through the origin. This projection is a fibration, and if V is given an inner product, the fibre containing U can be identified with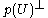
, the orthogonal complement to p(U).
The fibres are therefore vector spaces, and the projection p is a vector bundle
over the Grassmannian
, which defines the manifold
structure on Graffk(V).
As a homogeneous space
, the affine Grassmannian of an n-dimensional vector space V can be identified with
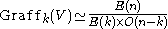
where E(n) is the Euclidean group
of Rn and O(m) is the orthogonal group
on Rm. It follows that the dimension is given by
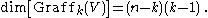
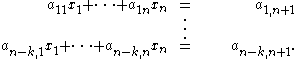
These determine a rank n−k system of linear equations on Rn+1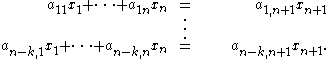
whose solution is a (k+1)-plane that, when intersected with xn+1 = 1, is the original k-plane.
Because of this identification, Graff(k,n) is a Zariski open set in Gr(k+1,n+1).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there are two distinct meanings of the term affine Grassmannian. In one it is the manifold of all k-dimensional affine subspaces
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
of Rn (described on this page), while in the other the affine Grassmannian
Affine Grassmannian
In mathematics, the term affine Grassmannian has two distinct meanings. In one meaning the affine Grassmannian is the manifold of all k-dimensional affine subspaces of a finite dimensional vector space, while the affine Grassmannian of an algebraic group G over a field k is defined in one of two...
is a quotient of a group-ring based on formal Laurent series.
Formal definition
Given a finite-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V and a non-negative integer k, then Graffk(V) is the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of all affine
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
k-dimensional subspaces of V.
It has a natural projection p:Graffk(V) → Grk(V), the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of all linear k-dimensional subspaces of V by defining p(U) to be the translation of U to a subspace through the origin. This projection is a fibration, and if V is given an inner product, the fibre containing U can be identified with
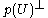, the orthogonal complement to p(U).The fibres are therefore vector spaces, and the projection p is a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
, which defines the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure on Graffk(V).
As a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
, the affine Grassmannian of an n-dimensional vector space V can be identified with
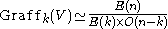
where E(n) is the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
of Rn and O(m) is the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
on Rm. It follows that the dimension is given by
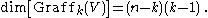
Relationship with ordinary Grassmannian
Let be the usual linear coordinates on Rn. Then Rn is embedded into Rn+1 as the affine hyperplane xn+1 = 1. The k-dimensional affine subspaces of Rn are in one-to-one correspondence with the linear subspaces of Rn+1 that are in general position with respect to the plane xn+1 = 1. Indeed, a k-dimensional affine subspace of Rn is the locus of solutions of a rank n k system of affine equations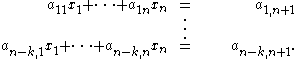These determine a rank n−k system of linear equations on Rn+1
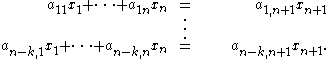
whose solution is a (k+1)-plane that, when intersected with xn+1 = 1, is the original k-plane.
Because of this identification, Graff(k,n) is a Zariski open set in Gr(k+1,n+1).