Affine hull
Encyclopedia
In mathematics
, the affine hull of a set S in Euclidean space
Rn is the smallest affine set containing S, or equivalently, the intersection
of all affine sets containing S. Here, an affine set may be defined as the translation of a vector subspace.
The affine hull aff(S) of S is the set of all affine combinations of elements of S, that is,
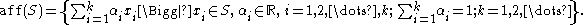
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the affine hull of a set S in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is the smallest affine set containing S, or equivalently, the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of all affine sets containing S. Here, an affine set may be defined as the translation of a vector subspace.
The affine hull aff(S) of S is the set of all affine combinations of elements of S, that is,
Examples
- The affine hull of a set of two different points is the line through them.
- The affine hull of a set of three points not on one line is the plane going through them.
- The affine hull of a set of four points not in a plane in R3 is the entire space R3.
Properties
-
-
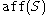is a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
Related sets
- If instead of an affine combination one uses a convex combinationConvex combinationIn convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
, that is one requires in the formula above that all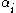
be non-negative, one obtains the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of S, which cannot be larger than the affine hull of S as more restrictions are involved. - The notion of conical combinationConical combinationGiven a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...
gives rise to the notion of the conical hull - If however one puts no restrictions at all on the numbers
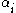, instead of an affine combination one has a linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
, and the resulting set is the linear spanLinear spanIn the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of S, which contains the affine hull of S.