.gif)
Alexander Macfarlane (mathematician)
Encyclopedia
Alexander Macfarlane FRSE (April 21, 1851 – August 28, 1913) was a Scottish
logic
ian, physicist
, and mathematician
.
Macfarlane was born in Blairgowrie
, Scotland
and studied at the University of Edinburgh
. His doctoral thesis, on the conditions governing the electric spark
, was subsequently published in the Transactions of the Royal Society of Edinburgh. It brought him to the notice of James Clerk Maxwell
, and in 1878 Macfarlane was elected a Fellow of the Royal Society of Edinburgh
During his life, Macfarlane played a prominent role in research and education. He taught at the universities of Edinburgh and St Andrews
, was physics professor
at the University of Texas
(1885 – 1894), professor of Advanced Electricity, and later of mathematical physics
, at Lehigh University
. MacFarlane was the secretary of the Quaternion Society and compiler of its publications.
Macfarlane was also the author of a popular 1916 collection of mathematical biographies (Ten British Mathematicians), a similar work on physicists (Lectures on Ten British Physicists of the Nineteenth Century, 1919), and he compiled a bibliography
on quaternion
s in 1904.
Macfarlane was caught up in the revolution in geometry
during his lifetime, in particular through the influence of G. B. Halsted
who was mathematics professor at the University of Texas. Macfarlane originated an Algebra of Physics, which was his adaptation of quaternions to physical science. His first publication on Space Analysis preceded the presentation of Minkowski Space
by seventeen years.
Macfarlane actively participated in several International Congresses of Mathematicians
including the primordial meeting in Chicago, 1893, and the Paris meeting of 1900 where he spoke on "Application of space analysis to curvilinear coordinates".
Macfarlane retired to Chatham, Ontario
, where he died in 1913.
Page numbers are carried from previous publications, and the reader is presumed familiar with quaternions. The first paper is "Principles of the Algebra of Physics" where he first proposes the hyperbolic quaternion
algebra, since "a student of physics finds a difficulty in principle of quaternions which makes the square of a vector negative." The second paper is "The Imaginary of the Algebra". Here he introduces the hyperbolic versor as the hyperbolic quaternion corresponding to the versor of Hamilton. The presentation is encumbered by the notation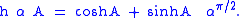
Later he conformed to the notation exp(A α) used by Euler and Sophus Lie. The expression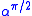
is meant to emphasize that α is a right versor, where π/2 is the measure of a right angle
in radian
s. The π/2 in the exponent is, in fact, superfluous.
Papers three and four are "Fundamental Theorems of Analysis Generalized for Space" and "On the definition of the Trigonometric Functions", which he had presented the previous year in Chicago at the Congress of Mathematicians held in connection with the World's Columbian Exhibition. He follows George Salmon
in exhibiting the hyperbolic angle
, argument of hyperbolic function
s. The fifth paper is "Elliptic and Hyperbolic Analysis" which considers the spherical law of cosines as the fundamental theorem of the sphere
, and proceeds to analogues for the ellipsoid of revolution, general ellipsoid, and equilateral hyperboloids of one and two sheets, where he provides the hyperbolic law of cosines.
In 1900 Alexander published "Hyperbolic Quaternions" with the Royal Society in Edinburgh, and included a sheet of nine figures, two of which display conjugate hyperbola
s. Having been stung in the Great Vector Debate over the non-associativity of his Algebra of Physics, he restored associativity by reverting to biquaternions, an algebra used by students of Hamilton since 1853.
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
ian, physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
, and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
.
Macfarlane was born in Blairgowrie
Blairgowrie and Rattray
Blairgowrie and Rattray and Raitear is possibly from an English language cognate of Gaelic ràth, meaning fortress + a Pictish term cognate with Welsh tref, meaning settlement) is a twin burgh in Perth and Kinross, Scotland. Amongst locals, the town is colloquially known simply as "Blair"...
, Scotland
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
and studied at the University of Edinburgh
University of Edinburgh
The University of Edinburgh, founded in 1583, is a public research university located in Edinburgh, the capital of Scotland, and a UNESCO World Heritage Site. The university is deeply embedded in the fabric of the city, with many of the buildings in the historic Old Town belonging to the university...
. His doctoral thesis, on the conditions governing the electric spark
Electric spark
An electric spark is a type of electrostatic discharge that occurs when an electric field creates an ionized electrically conductive channel in air producing a brief emission of light and sound. A spark is formed when the electric field strength exceeds the dielectric field strength of air...
, was subsequently published in the Transactions of the Royal Society of Edinburgh. It brought him to the notice of James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, and in 1878 Macfarlane was elected a Fellow of the Royal Society of Edinburgh
During his life, Macfarlane played a prominent role in research and education. He taught at the universities of Edinburgh and St Andrews
University of St Andrews
The University of St Andrews, informally referred to as "St Andrews", is the oldest university in Scotland and the third oldest in the English-speaking world after Oxford and Cambridge. The university is situated in the town of St Andrews, Fife, on the east coast of Scotland. It was founded between...
, was physics professor
Professor
A professor is a scholarly teacher; the precise meaning of the term varies by country. Literally, professor derives from Latin as a "person who professes" being usually an expert in arts or sciences; a teacher of high rank...
at the University of Texas
University of Texas at Austin
The University of Texas at Austin is a state research university located in Austin, Texas, USA, and is the flagship institution of the The University of Texas System. Founded in 1883, its campus is located approximately from the Texas State Capitol in Austin...
(1885 – 1894), professor of Advanced Electricity, and later of mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, at Lehigh University
Lehigh University
Lehigh University is a private, co-educational university located in Bethlehem, Pennsylvania, in the Lehigh Valley region of the United States. It was established in 1865 by Asa Packer as a four-year technical school, but has grown to include studies in a wide variety of disciplines...
. MacFarlane was the secretary of the Quaternion Society and compiler of its publications.
Macfarlane was also the author of a popular 1916 collection of mathematical biographies (Ten British Mathematicians), a similar work on physicists (Lectures on Ten British Physicists of the Nineteenth Century, 1919), and he compiled a bibliography
Bibliography
Bibliography , as a practice, is the academic study of books as physical, cultural objects; in this sense, it is also known as bibliology...
on quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s in 1904.
Macfarlane was caught up in the revolution in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
during his lifetime, in particular through the influence of G. B. Halsted
G. B. Halsted
George Bruce Halsted was a mathematician who explored foundations of geometry and introduced Non-Euclidean geometry into the United States through his own work and his many important translations...
who was mathematics professor at the University of Texas. Macfarlane originated an Algebra of Physics, which was his adaptation of quaternions to physical science. His first publication on Space Analysis preceded the presentation of Minkowski Space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
by seventeen years.
Macfarlane actively participated in several International Congresses of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
including the primordial meeting in Chicago, 1893, and the Paris meeting of 1900 where he spoke on "Application of space analysis to curvilinear coordinates".
Macfarlane retired to Chatham, Ontario
Chatham, Ontario
Chatham is the largest community in the municipality of Chatham-Kent, Ontario. Formerly serving as the seat of Kent County, the governments of the former city of Chatham, the county of Kent, and its townships were merged into one entity known as the Municipality of Chatham-Kent in 1998.Located on...
, where he died in 1913.
Space analysis
Alexander Macfarlane stylized his work as "Space Analysis". In 1894 he published his five earlier papers and a book review of Alexander MacAulay’s Utility of Quaternions in Physics. This collection is now available on-line.Page numbers are carried from previous publications, and the reader is presumed familiar with quaternions. The first paper is "Principles of the Algebra of Physics" where he first proposes the hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
algebra, since "a student of physics finds a difficulty in principle of quaternions which makes the square of a vector negative." The second paper is "The Imaginary of the Algebra". Here he introduces the hyperbolic versor as the hyperbolic quaternion corresponding to the versor of Hamilton. The presentation is encumbered by the notation
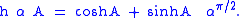
Later he conformed to the notation exp(A α) used by Euler and Sophus Lie. The expression
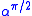is meant to emphasize that α is a right versor, where π/2 is the measure of a right angleRight angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. The π/2 in the exponent is, in fact, superfluous.
Papers three and four are "Fundamental Theorems of Analysis Generalized for Space" and "On the definition of the Trigonometric Functions", which he had presented the previous year in Chicago at the Congress of Mathematicians held in connection with the World's Columbian Exhibition. He follows George Salmon
George Salmon
The Reverend George Salmon was an Irish mathematician and theologian. His publications in algebraic geometry were widely read in the second half of the 19th century, but he devoted himself mostly to theology for the last forty years of his life...
in exhibiting the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
, argument of hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s. The fifth paper is "Elliptic and Hyperbolic Analysis" which considers the spherical law of cosines as the fundamental theorem of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, and proceeds to analogues for the ellipsoid of revolution, general ellipsoid, and equilateral hyperboloids of one and two sheets, where he provides the hyperbolic law of cosines.
In 1900 Alexander published "Hyperbolic Quaternions" with the Royal Society in Edinburgh, and included a sheet of nine figures, two of which display conjugate hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s. Having been stung in the Great Vector Debate over the non-associativity of his Algebra of Physics, he restored associativity by reverting to biquaternions, an algebra used by students of Hamilton since 1853.