Algebraic fraction
Encyclopedia
In elementary algebra
, an algebraic fraction is the indicated quotient
of two algebraic expression
s. Two examples of algebraic fractions are
and 
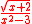. Algebraic fractions are subject to the same laws as arithmetic fractions.
, the dividend a is called the numerator and the divisor b is called the denominator. The numerator and denominator are called the terms
of the algebraic fraction.
A complex fraction is a fraction whose numerator or denominator, or both, contains a fraction. A simple fraction contains no fraction either in its numerator or its denominator. A fraction is in lowest terms if the only factor common to the numerator and the denominator is 1.
An expression which is not in fractional form is an integral expression. An integral expression can always be written in fractional form by giving it the denominator 1. A mixed expression is the algebraic sum of one or more integral expressions and one or more fractional terms.
s, the algebraic fraction is called a rational algebraic fraction or simply rational fraction. Rational fractions are also known under the term rational function
or rational expression. A rational fraction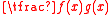
is called proper if 
, and improper otherwise. For example, the rational fraction 
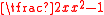is proper, and the rational fractions 
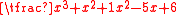and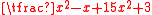 
are improper. Any improper rational fraction can be expressed as the sum of a polynomial (possibly constant) and a proper rational fraction. In the first example of an improper fraction one has
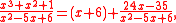
where the second term is a proper rational fraction. The sum of two proper rational fractions is a proper rational fraction as well. The reverse process of expressing a proper rational fraction as the sum of two or more fractions is called resolving it into partial fraction
s. For example,
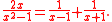
Here, the two terms on the right are called partial fractions.
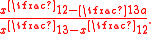
The process of transforming an irrational fraction to a rational fraction is known as rationalization
. Every irrational fraction in which the radicals are monomial
s may be rationalized by finding the least common multiple
of the indices of the roots, and substituting the variable for another variable with the least common multiple as exponent. In the example given, the least common multiple is 6, hence we can substitute
to obtain
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, an algebraic fraction is the indicated quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of two algebraic expression
Algebraic expression
In mathematics, an algebraic expression is an expression that contains only algebraic numbers, variables and algebraic operations. Algebraic operations are addition, subtraction, multiplication, division and exponentiation with integral or fractional exponents...
s. Two examples of algebraic fractions are
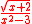and . Algebraic fractions are subject to the same laws as arithmetic fractions.Terminology
In the algebraic fraction, the dividend a is called the numerator and the divisor b is called the denominator. The numerator and denominator are called the termsTerm (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
of the algebraic fraction.
A complex fraction is a fraction whose numerator or denominator, or both, contains a fraction. A simple fraction contains no fraction either in its numerator or its denominator. A fraction is in lowest terms if the only factor common to the numerator and the denominator is 1.
An expression which is not in fractional form is an integral expression. An integral expression can always be written in fractional form by giving it the denominator 1. A mixed expression is the algebraic sum of one or more integral expressions and one or more fractional terms.
Rational fractions
If the expressions a and b are polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, the algebraic fraction is called a rational algebraic fraction or simply rational fraction. Rational fractions are also known under the term rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
or rational expression. A rational fraction
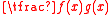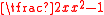is called proper if , and improper otherwise. For example, the rational fraction is proper, and the rational fractions 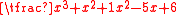and 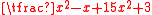are improper. Any improper rational fraction can be expressed as the sum of a polynomial (possibly constant) and a proper rational fraction. In the first example of an improper fraction one has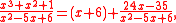where the second term is a proper rational fraction. The sum of two proper rational fractions is a proper rational fraction as well. The reverse process of expressing a proper rational fraction as the sum of two or more fractions is called resolving it into partial fraction
Partial fraction
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
s. For example,
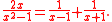
Here, the two terms on the right are called partial fractions.
Irrational fractions
An irrational fraction is one that contains the variable under a fractional exponent. An example of an irrational fraction is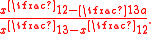The process of transforming an irrational fraction to a rational fraction is known as rationalization
Rationalisation (mathematics)
In elementary algebra, root rationalisation is a process by which surds in the denominator of an irrational fraction are eliminated.These surds may be monomials or binomials involving square roots, in simple examples...
. Every irrational fraction in which the radicals are monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s may be rationalized by finding the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the indices of the roots, and substituting the variable for another variable with the least common multiple as exponent. In the example given, the least common multiple is 6, hence we can substitute
to obtain