An alternated square tiling is another square tiling, but having two types of squares, alternating in a checkerboard Checkerboard A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....  pattern.	valign=top| A twice alternated square tiling.
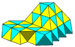A partially-filled alternated cubic honeycomb with tetrahedral and octahedral cells.	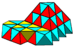A subsymmetry colored alternated cubic honeycomb.

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the alternated hypercube honeycomb (or demicubic honeycomb) is a dimensional infinite series of honeycomb

Honeycomb (geometry)

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

s, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group 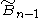 for n ≥ 4. A lower symmetry form 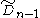can be created by removing another mirror on a order-4 peak

Peak (geometry)

In geometry, a peak is an -face of an n-dimensional polytope. A peak attaches at least three facets ....

.

The alternated hypercube facets become demihypercubes, and the deleted vertices create new orthoplex facets. The vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 for honeycombs of this family are rectified

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 orthoplexes.

These are also named as hδ_n for an (n-1)-dimensional honeycomb.

hδn	Name	Schläfli symbol	Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
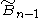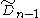hδ2	Apeirogon Apeirogon An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...	{∞}
hδ3	Alternated square tiling (Same as regular square tiling {4,4})	h{4,4}=t1{4,4} t0,2{4,4}
hδ4	Alternated cubic honeycomb	h{4,3,4} {31,1,4}
hδ5	Alternated tesseractic honeycomb or demitesseractic tetracomb Demitesseractic tetracomb In four-dimensional Euclidean geometry, the 16-cell honeycomb is the one of three regular space-filling tessellation in Euclidean 4-space. The other two are the tesseractic honeycomb and the 24-cell honeycomb. This honeycomb is constructed from 16-cell facets, three around every edge... (Same as regular {3,3,4,3})	h{4,32,4} {31,1,3,4} {31,1,1,1}
hδ6	Demipenteractic honeycomb	h{4,33,4} {31,1,32,4} {31,1,3,31,1}
hδ7	Demihexeractic honeycomb	h{4,34,4} {31,1,33,4} {31,1,32,31,1}
hδ8	Demihepteractic honeycomb	h{4,35,4} {31,1,34,4} {31,1,33,31,1}
hδ9	Demiocteractic honeycomb	h{4,36,4} {31,1,35,4} {31,1,34,31,1}
hδ10	Demienneractic honeycomb	h{4,37,4} {31,1,36,4} {31,1,35,31,1}
hδ11	Demidekeractic honeycomb	h{4,38,4} {31,1,37,4} {31,1,36,31,1}
hδn	n-demicubic honeycomb	h{4,3n-3,4} {31,1,3n-4,4} {31,1,3n-5,31,1}	...