
Demitesseractic tetracomb
Encyclopedia
Perspective projection: the first layer of adjacent 16-cell facets. |
|
| Type | Regular 4-space honeycomb |
| Family | Alternated hypercube honeycomb |
| Schläfli symbol | {3,3,4,3} h{4,3,3,4} h0,4{4,3,3,4} {31,1,3,4} h{4,3,31,1} {31,1,1,1} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| 4-face type | {3,3,4} 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
| Cell type | {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| Face type | {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Edge figure | cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
24-cell (Rectified 16-cell) |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
[3,4,3,3] [4,3,31,1] [31,1,1,1] |
| Dual | {3,4,3,3} |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
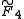 , [3,4,3,3] , [3,4,3,3]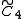 , [4,3,3,4] , [4,3,3,4]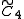 , [4,(3,3)+,4] , [4,(3,3)+,4]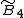 , [4,3,31,1] , [4,3,31,1]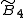 , [4,(3,31,1)+] , [4,(3,31,1)+]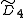 , [31,1,1,1] , [31,1,1,1] |
| Properties | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... , edge-transitive, face-transitive, cell-transitive |
In four-dimensional Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the 16-cell honeycomb is the one of three regular space-filling tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
(or honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) in Euclidean 4-space. The other two are the tesseractic honeycomb and the 24-cell honeycomb. This honeycomb is constructed from 16-cell
16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
facet
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
s, three around every edge. It has a 24-cell vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
.
This vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
or lattice is called the B4, D4, or F4 lattice.
Alternate names
- Hexadecachoric tetracomb / Hexadecachoric honeycomb
- Demitesseractic tetracomb / Demitesseractic honeycomb
Coordinates
As a regular honeycomb, {3,3,4,3}, it has no lower dimensional analogues, but as an alternated form (the demitesseractic honeycomb, h{4,3,3,4}) it is related to the alternated cubic honeycomb.Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even.
Kissing number
The vertices of this tessellation are the centers of the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
s in the densest possible packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
of equal spheres in 4-space; its kissing number is 24, which is also the highest possible in 4-space.
See also
- Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycombTruncated 24-cell honeycombIn four-dimensional Euclidean geometry, the truncated 24-cell honeycomb is a uniform space-filling honeycomb. It can be seen as a truncation of the regular 24-cell honeycomb, containing tesseract and truncated 24-cell cells....
- Snub 24-cell honeycombSnub 24-cell honeycombIn four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes...
- 5-cell honeycomb5-cell honeycombIn four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb...
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
- k-demicubic honeycombs:
- Alternated cubic honeycomb
- 4-demicubic honeycomb
- 5-demicubic honeycomb
- 6-demicubic honeycomb
- 7-demicubic honeycomb
- 8-demicubic honeycomb

