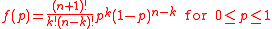An Essay towards solving a Problem in the Doctrine of Chances
Encyclopedia
An Essay towards solving a Problem in the Doctrine of Chances is a work on the mathematical theory of probability by the Reverend Thomas Bayes
, published in 1763, two years after its author's death. It included a statement of a special case of what is now called Bayes' theorem
. In 18th-century English, the phrase "doctrine of chances" meant the theory of probability. It had been introduced as the title of a book
by Abraham de Moivre
.
Bayes supposed a sequence of independent experiments, each having as its outcome either success or failure, the probability of success being some number p between 0 and 1. But then he supposed p to be an uncertain quantity, whose probability of being in any interval between 0 and 1 is the length of the interval. In modern terms, p would be considered a random variable
uniformly distributed between 0 and 1. Conditionally on the value of p
, the trials resulting in success or failure are independent, but unconditionally (or "marginally
") they are not. That is because if a large number of successes are observed, then p is more likely to be large, so that success on the next trial is more probable. The question Bayes addressed was: what is the conditional probability distribution of p, given the numbers of successes and failures so far observed. The answer is that its probability density function
is
(and ƒ(p) = 0 for p < 0 or p > 1) where k is the number of successes so far observed, and n is the number of trials so far observed. This is what today is called the Beta distribution with parameters k + 1 and n − k + 1.
Thomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
, published in 1763, two years after its author's death. It included a statement of a special case of what is now called Bayes' theorem
Bayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
. In 18th-century English, the phrase "doctrine of chances" meant the theory of probability. It had been introduced as the title of a book
The Doctrine of Chances
The Doctrine of Chances was the first textbook on probability theory, written by 18th-century French mathematician Abraham de Moivre and first published in 1718. De Moivre wrote in English because he resided in England at the time, having fled France to escape the persecution of Huguenots...
by Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
.
Bayes supposed a sequence of independent experiments, each having as its outcome either success or failure, the probability of success being some number p between 0 and 1. But then he supposed p to be an uncertain quantity, whose probability of being in any interval between 0 and 1 is the length of the interval. In modern terms, p would be considered a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
uniformly distributed between 0 and 1. Conditionally on the value of p
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
, the trials resulting in success or failure are independent, but unconditionally (or "marginally
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
") they are not. That is because if a large number of successes are observed, then p is more likely to be large, so that success on the next trial is more probable. The question Bayes addressed was: what is the conditional probability distribution of p, given the numbers of successes and failures so far observed. The answer is that its probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
(and ƒ(p) = 0 for p < 0 or p > 1) where k is the number of successes so far observed, and n is the number of trials so far observed. This is what today is called the Beta distribution with parameters k + 1 and n − k + 1.
External links
- An Essay towards solving a Problem in the Doctrine of Chances at the UCLA Department of Statistics