
Analytic Hierarchy Process
Encyclopedia
The Analytic Hierarchy Process (AHP) is a structured technique for organizing and analyzing complex decisions. Based on mathematics
and psychology
, it was developed by Thomas L. Saaty in the 1970s and has been extensively studied and refined since then.
It has particular application in group decision making
, and is used around the world in a wide variety of decision situations
, in fields such as government
, business
, industry
, healthcare, and education
.
Rather than prescribing a "correct" decision, the AHP helps decision makers find one that best suits their goal and their understanding of the problem. It provides a comprehensive and rational framework for structuring a decision problem, for representing and quantifying its elements, for relating those elements to overall goals, and for evaluating alternative solutions.
Users of the AHP first decompose their decision problem into a hierarchy
of more easily comprehended sub-problems, each of which can be analyzed independently. The elements of the hierarchy can relate to any aspect of the decision problem—tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood—anything at all that applies to the decision at hand.
Once the hierarchy is built, the decision makers systematically evaluate its various elements by comparing them to one another two at a time, with respect to their impact on an element above them in the hierarchy. In making the comparisons, the decision makers can use concrete data about the elements, but they typically use their judgments about the elements' relative meaning and importance. It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations.
The AHP converts these evaluations to numerical values that can be processed and compared over the entire range of the problem. A numerical weight or priority
is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way. This capability distinguishes the AHP from other decision making techniques.
In the final step of the process, numerical priorities are calculated for each of the decision alternatives. These numbers represent the alternatives' relative ability to achieve the decision goal, so they allow a straightforward consideration of the various courses of action.
Several firms supply computer software
to assist in using the process.
It has unique advantages when important elements of the decision are difficult to quantify or compare, or where communication among team members is impeded by their different specializations, terminologies, or perspectives.
Decision situations to which the AHP can be applied include:
The applications of AHP to complex decision
situations have numbered in the thousands, and have produced extensive results in problems involving planning
, resource allocation
, priority setting, and selection among alternatives. Other areas have included forecasting
, total quality management
, business process re-engineering
, quality function deployment
, and the Balanced Scorecard
. Many AHP applications are never reported to the world at large, because they take place at high levels of large organizations where security
and privacy
considerations prohibit their disclosure. But some uses of AHP are discussed in the literature
. Recently these have included:
AHP is sometimes used in designing highly specific procedures for particular situations, such as the rating of buildings by historic significance. It was recently applied to a project that uses video
footage to assess the condition of highways in Virginia
. Highway engineers first used it to determine the optimum scope of the project
, then to justify its budget
to lawmakers.
, it is considered an important subject in many institutions of higher learning, including schools of engineering
and graduate schools of business
. It is a particularly important subject in the quality field, and is taught in many specialized courses including Six Sigma
, Lean Six Sigma
, and QFD
.
The value of the AHP is recognized in developed and developing countries around the world. China is a good example — nearly a hundred Chinese universities offer courses in AHP, and many doctoral students choose AHP as the subject of their research
and dissertations. Over 900 papers have been published on the subject in China, and there is at least one Chinese scholarly journal devoted exclusively to AHP.
The International Symposium on the Analytic Hierarchy Process
(ISAHP) holds biennial meetings of academics and practitioners interested in the field. A wide range of topics are covered. Those in 2005 ranged from Establishing Payment Standards for Surgical Specialists, to Strategic Technology Roadmapping, to Infrastructure Reconstruction in Devastated Countries.
At the 2007 meeting in Valparaíso, Chile, over 90 papers were presented from 19 countries, including the U.S., Germany, Japan, Chile
, Malaysia, and Nepal
. A similar number of papers were presented at the 2009 symposium in Pittsburgh, Pennsylvania
, when 28 countries were represented. Subjects of the papers included Economic Stabilization in Latvia, Portfolio Selection in the Banking Sector, Wildfire Management to Help Mitigate Global Warming, and Rural Microprojects in Nepal.
 As can be seen in the material that follows, using the AHP involves the mathematical synthesis of numerous judgments about the decision problem at hand. It is not uncommon for these judgments to number in the dozens or even the hundreds. While the math can be done by hand or with a calculator, it is far more common to use one of several computerized methods for entering and synthesizing the judgments. The simplest of these involve standard spreadsheet software, while the most complex use custom software, often augmented by special devices for acquiring the judgments of decision makers gathered in a meeting room.
As can be seen in the material that follows, using the AHP involves the mathematical synthesis of numerous judgments about the decision problem at hand. It is not uncommon for these judgments to number in the dozens or even the hundreds. While the math can be done by hand or with a calculator, it is far more common to use one of several computerized methods for entering and synthesizing the judgments. The simplest of these involve standard spreadsheet software, while the most complex use custom software, often augmented by special devices for acquiring the judgments of decision makers gathered in a meeting room.
The procedure for using the AHP can be summarized as:
These steps are more fully described below.
Human organizations are often structured as hierarchies, where the hierarchical system is used for assigning responsibilities, exercising leadership, and facilitating communication. Familiar hierarchies of "things" include a desktop computer's tower unit at the "top", with its subordinate monitor, keyboard, and mouse "below."
In the world of ideas, we use hierarchies to help us acquire detailed knowledge of complex reality: we structure the reality into its constituent parts, and these in turn into their own constituent parts, proceeding down the hierarchy as many levels as we care to. At each step, we focus on understanding a single component of the whole, temporarily disregarding the other components at this and all other levels. As we go through this process, we increase our global understanding of whatever complex reality we are studying.
Think of the hierarchy that medical students use while learning anatomy—they separately consider the musculoskeletal system (including parts and subparts like the hand and its constituent muscles and bones), the circulatory system (and its many levels and branches), the nervous system (and its numerous components and subsystems), etc., until they've covered all the systems and the important subdivisions of each. Advanced students continue the subdivision all the way to the level of the cell or molecule. In the end, the students understand the "big picture" and a considerable number of its details. Not only that, but they understand the relation of the individual parts to the whole. By working hierarchically, they've gained a comprehensive understanding of anatomy.
Similarly, when we approach a complex decision problem, we can use a hierarchy to integrate large amounts of information into our understanding of the situation. As we build this information structure, we form a better and better picture of the problem as a whole.
Published descriptions of AHP applications often include diagrams and descriptions of their hierarchies; some simple ones are shown throughout this article. More complex AHP hierarchies have been collected and reprinted in at least one book. More complex hierarchies can be found in this article's talk page.
The design of any AHP hierarchy will depend not only on the nature of the problem at hand, but also on the knowledge, judgments, values, opinions, needs, wants, etc. of the participants in the decision making process. Constructing a hierarchy typically involves significant discussion, research, and discovery by those involved. Even after its initial construction, it can be changed to accommodate newly-thought-of criteria or criteria not originally considered to be important; alternatives can also be added, deleted, or changed.
To better understand AHP hierarchies, consider a decision problem with a goal to be reached, three alternative ways of reaching the goal, and four criteria against which the alternatives need to be measured.
Such a hierarchy can be visualized as a diagram like the one immediately below, with the goal at the top, the three alternatives at the bottom, and the four criteria in between. There are useful terms for describing the parts of such diagrams: Each box is called a node. A node that is connected to one or more nodes in a level below it is called a parent node. The nodes to which it is so connected are called its children.
Applying these definitions to the diagram below, the Goal is the parent of the four Criteria, and the four Criteria are children of the Goal. Each Criterion is a parent of the three Alternatives. Note that there are only three Alternatives, but in the diagram, each of them is repeated under each of its parents.
To reduce the size of the drawing required, it is common to represent AHP hierarchies as shown in the diagram below, with only one node for each alternative, and with multiple lines connecting the alternatives and the criteria that apply to them. To avoid clutter, these lines are sometimes omitted or reduced in number. Regardless of any such simplifications in the diagram, in the actual hierarchy each alternative is connected to every one of its parent nodes.
Consider the "Choose a Leader" example above. An important task of the decision makers is to determine the weight to be given each criterion in making the choice of a leader. Another important task is to determine the weight to be given to each candidate with regard to each of the criteria. The AHP not only lets them do that, but it lets them put a meaningful and objective numerical value on each of the four criteria.
Like probabilities, priorities are absolute number
s between zero and one, without units or dimensions. A node with priority .200 has twice the weight in reaching the goal as one with priority .100, ten times the weight of one with priority .020, and so forth. Depending on the problem at hand, "weight" can refer to importance, or preference, or likelihood, or whatever factor is being considered by the decision makers.
Priorities are distributed over a hierarchy according to its architecture, and their values depend on the information entered by users of the process. Priorities of the Goal, the Criteria, and the Alternatives are intimately related, but need to be considered separately.
By definition, the priority of the Goal is 1.000. The priorities of the Alternatives always add up to 1.000. Things can become complicated with multiple levels of Criteria, but if there is only one level, their priorities also add to 1.000. All this is illustrated by the priorities in the example below.
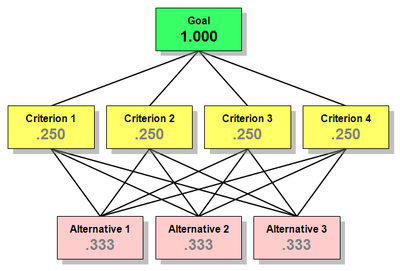 Observe that the priorities on each level of the example—the Goal, the Criteria, and the Alternatives—all add up to 1.000.
Observe that the priorities on each level of the example—the Goal, the Criteria, and the Alternatives—all add up to 1.000.
The priorities shown are those that exist before any information has been entered about weights of the criteria or alternatives, so the priorities within each level are all equal. They are called the hierarchy's default priorities. If a fifth Criterion were added to this hierarchy, the default priority for each Criterion would be .200. If there were only two Alternatives, each would have a default priority of .500.
Two additional concepts apply when a hierarchy has more than one level of criteria: local priorities and global priorities. Consider the hierarchy shown below, which has several Subcriteria under each Criterion.
 The local priorities, shown in gray, represent the relative weights of the nodes within a group of siblings with respect to their parent. You can easily see that the local priorities of each group of Criteria and their sibling Subcriteria add up to 1.000. The global priorities, shown in black, are obtained by multiplying the local priorities of the siblings by their parent's global priority. The global priorities for all the subcriteria in the level add up to 1.000.
The local priorities, shown in gray, represent the relative weights of the nodes within a group of siblings with respect to their parent. You can easily see that the local priorities of each group of Criteria and their sibling Subcriteria add up to 1.000. The global priorities, shown in black, are obtained by multiplying the local priorities of the siblings by their parent's global priority. The global priorities for all the subcriteria in the level add up to 1.000.
The rule is this: Within a hierarchy, the global priorities of child nodes always add up to the global priority of their parent. Within a group of children, the local priorities add up to 1.000.
So far, we have looked only at default priorities. As the Analytical Hierarchy Process moves forward, the priorities will change from their default values as the decision makers input information about the importance of the various nodes. They do this by making a series of pairwise comparisons.
, specifically designed as in-depth teaching examples, are provided as appendices to this article:
Some of the books on AHP contain practical examples of its use, though they are not typically intended to be step-by-step learning aids. One of them contains a handful of expanded examples, plus about 400 AHP hierarchies briefly described and illustrated with figures. Many examples are discussed, mostly for professional audiences, in papers published by the International Symposium on the Analytic Hierarchy Process
.
and management science textbooks, and is taught in numerous universities; it is used extensively in organizations that have carefully investigated its theoretical underpinnings. While the general consensus is that it is both technically valid and practically useful, the method does have its critics. Most of the criticisms involve a phenomenon called rank reversal, discussed in the following section.
Rank reversal
Decision making involves ranking alternatives in terms of criteria or attributes of those alternatives. It is an axiom of some decision theories that when new alternatives are added to a decision problem, the ranking of the old alternatives must not change — that "rank reversal" must not occur.
The reasonableness of this axiom for all applications is questionable, since there are real-world examples where adding new alternatives can change the rank of the old ones. There are also situations where it is not reasonable for the rank of existing alternatives to change when a new alternative that is not as good as any of the existing alternatives is added for consideration.
The 2000 U.S. presidential election
is an example of a decision that can be understood as involving rank reversal. Ralph Nader
was an 'irrelevant' alternative, in that he was dominated by both the Democrat
and Republican
candidates. However, since he may have attracted more votes from those who would have voted Democratic rather than Republican, his presence caused the ranks to reverse. Put another way, if Nader were not in the race, it is conceivable that Al Gore
would have won. The same could be said for the impact that Ross Perot had on George Bush's loss in 1992.
There are two schools of thought about rank reversal. One maintains that new alternatives that introduce no additional attributes should not cause rank reversal under any circumstances. The other maintains that there are some situations in which rank reversal can reasonably be expected. The original formulation of AHP allowed rank reversals. In 1993, Forman introduced a second AHP synthesis mode, called the ideal synthesis mode, to address choice situations in which the addition or removal of an 'irrelevant' alternative should not and will not cause a change in the ranks of existing alternatives. The current version of the AHP can accommodate both these schools — its Ideal Mode preserves rank, while its Distributive Mode allows the ranks to change. Either mode is selected according to the problem at hand.
Rank reversal and the AHP are extensively discussed in a 2001 paper in Operations Research, as well as a chapter entitled Rank Preservation and Reversal, in the current basic book on AHP. The latter presents published examples of rank reversal due to adding copies and near copies of an alternative, due to intransitivity of decision rules, due to adding phantom and decoy alternatives, and due to the switching phenomenon in utility functions. It also discusses the Distributive and Ideal Modes of the AHP.
These books also provide useful information about the AHP and its applications:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
, it was developed by Thomas L. Saaty in the 1970s and has been extensively studied and refined since then.
It has particular application in group decision making
Group decision making
Group decision making is a situation faced when individuals are brought together in a group to solve problems. According to the idea of synergy, decisions made collectively tend to be more effective than decisions made by a single individual...
, and is used around the world in a wide variety of decision situations
Decision making
Decision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
, in fields such as government
Government
Government refers to the legislators, administrators, and arbitrators in the administrative bureaucracy who control a state at a given time, and to the system of government by which they are organized...
, business
Business
A business is an organization engaged in the trade of goods, services, or both to consumers. Businesses are predominant in capitalist economies, where most of them are privately owned and administered to earn profit to increase the wealth of their owners. Businesses may also be not-for-profit...
, industry
Industry
Industry refers to the production of an economic good or service within an economy.-Industrial sectors:There are four key industrial economic sectors: the primary sector, largely raw material extraction industries such as mining and farming; the secondary sector, involving refining, construction,...
, healthcare, and education
Education
Education in its broadest, general sense is the means through which the aims and habits of a group of people lives on from one generation to the next. Generally, it occurs through any experience that has a formative effect on the way one thinks, feels, or acts...
.
Rather than prescribing a "correct" decision, the AHP helps decision makers find one that best suits their goal and their understanding of the problem. It provides a comprehensive and rational framework for structuring a decision problem, for representing and quantifying its elements, for relating those elements to overall goals, and for evaluating alternative solutions.
Users of the AHP first decompose their decision problem into a hierarchy
Hierarchy
A hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
of more easily comprehended sub-problems, each of which can be analyzed independently. The elements of the hierarchy can relate to any aspect of the decision problem—tangible or intangible, carefully measured or roughly estimated, well- or poorly-understood—anything at all that applies to the decision at hand.
Once the hierarchy is built, the decision makers systematically evaluate its various elements by comparing them to one another two at a time, with respect to their impact on an element above them in the hierarchy. In making the comparisons, the decision makers can use concrete data about the elements, but they typically use their judgments about the elements' relative meaning and importance. It is the essence of the AHP that human judgments, and not just the underlying information, can be used in performing the evaluations.
The AHP converts these evaluations to numerical values that can be processed and compared over the entire range of the problem. A numerical weight or priority
Priority
Priority may refer to:* Priority date, a concept of establishing waiting times in the immigration process by United States Department of State* Priority level, the priority of emergency communications...
is derived for each element of the hierarchy, allowing diverse and often incommensurable elements to be compared to one another in a rational and consistent way. This capability distinguishes the AHP from other decision making techniques.
In the final step of the process, numerical priorities are calculated for each of the decision alternatives. These numbers represent the alternatives' relative ability to achieve the decision goal, so they allow a straightforward consideration of the various courses of action.
Several firms supply computer software
Computer software
Computer software, or just software, is a collection of computer programs and related data that provide the instructions for telling a computer what to do and how to do it....
to assist in using the process.
Uses and applications
While it can be used by individuals working on straightforward decisions, the Analytic Hierarchy Process (AHP) is most useful where teams of people are working on complex problems, especially those with high stakes, involving human perceptions and judgments, whose resolutions have long-term repercussions.It has unique advantages when important elements of the decision are difficult to quantify or compare, or where communication among team members is impeded by their different specializations, terminologies, or perspectives.
Decision situations to which the AHP can be applied include:
- Choice - The selection of one alternative from a given set of alternatives, usually where there are multiple decision criteria involved.
- RankingRankingA ranking is a relationship between a set of items such that, for any two items, the first is either 'ranked higher than', 'ranked lower than' or 'ranked equal to' the second....
- Putting a set of alternatives in order from most to least desirable - Prioritization - Determining the relative merit of members of a set of alternatives, as opposed to selecting a single one or merely ranking them
- Resource allocationResource allocationResource allocation is used to assign the available resources in an economic way. It is part of resource management. In project management, resource allocation is the scheduling of activities and the resources required by those activities while taking into consideration both the resource...
- Apportioning resources among a set of alternatives - BenchmarkingBenchmarkingBenchmarking is the process of comparing one's business processes and performance metrics to industry bests and/or best practices from other industries. Dimensions typically measured are quality, time and cost...
- Comparing the processes in one's own organization with those of other best-of-breed organizations - Quality managementQuality managementThe term Quality management has a specific meaning within many business sectors. This specific definition, which does not aim to assure 'good quality' by the more general definition , can be considered to have four main components: quality planning, quality control, quality assurance and quality...
- Dealing with the multidimensional aspects of quality and quality improvement - Conflict resolutionConflict resolutionConflict resolution is conceptualized as the methods and processes involved in facilitating the peaceful ending of some social conflict. Often, committed group members attempt to resolve group conflicts by actively communicating information about their conflicting motives or ideologies to the rest...
- Settling disputes between parties with apparently incompatible goals or positions
The applications of AHP to complex decision
Decision making
Decision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
situations have numbered in the thousands, and have produced extensive results in problems involving planning
Planning
Planning in organizations and public policy is both the organizational process of creating and maintaining a plan; and the psychological process of thinking about the activities required to create a desired goal on some scale. As such, it is a fundamental property of intelligent behavior...
, resource allocation
Resource allocation
Resource allocation is used to assign the available resources in an economic way. It is part of resource management. In project management, resource allocation is the scheduling of activities and the resources required by those activities while taking into consideration both the resource...
, priority setting, and selection among alternatives. Other areas have included forecasting
Forecasting
Forecasting is the process of making statements about events whose actual outcomes have not yet been observed. A commonplace example might be estimation for some variable of interest at some specified future date. Prediction is a similar, but more general term...
, total quality management
Total Quality Management
Total quality management or TQM is an integrative philosophy of management for continuously improving the quality of products and processes....
, business process re-engineering
Business Process Improvement
Business Process Improvement is a systematic approach to help an organization optimize its underlying processes to achieve more efficient results. The methodology was first documented in H. James Harrington’s 1991 book Business Process Improvement. It is the methodology that both Process...
, quality function deployment
Quality function deployment
Quality function deployment is a “method to transform user demands into design quality, to deploy the functions forming quality, and to deploy methods for achieving the design quality into subsystems and component parts, and ultimately to specific elements of the manufacturing process.”, as...
, and the Balanced Scorecard
Balanced scorecard
The Balanced Scorecard is a strategic performance management tool - a semi-standard structured report, supported by proven design methods and automation tools, that can be used by managers to keep track of the execution of activities by the staff within their control and to monitor the...
. Many AHP applications are never reported to the world at large, because they take place at high levels of large organizations where security
Security
Security is the degree of protection against danger, damage, loss, and crime. Security as a form of protection are structures and processes that provide or improve security as a condition. The Institute for Security and Open Methodologies in the OSSTMM 3 defines security as "a form of protection...
and privacy
Privacy
Privacy is the ability of an individual or group to seclude themselves or information about themselves and thereby reveal themselves selectively...
considerations prohibit their disclosure. But some uses of AHP are discussed in the literature
Scientific literature
Scientific literature comprises scientific publications that report original empirical and theoretical work in the natural and social sciences, and within a scientific field is often abbreviated as the literature. Academic publishing is the process of placing the results of one's research into the...
. Recently these have included:
- Deciding how best to reduce the impact of global climate changeClimate changeClimate change is a significant and lasting change in the statistical distribution of weather patterns over periods ranging from decades to millions of years. It may be a change in average weather conditions or the distribution of events around that average...
(Fondazione Eni Enrico Mattei) - QuantifyingQuantificationQuantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
the overall quality of software systemSoftware systemA software system is a system based on software forming part of a computer system . The term "software system" is often used as a synonym of computer program or software; is related to the application of systems theory approaches in software engineering context and are used to study large and...
s (Microsoft Corporation) - Selecting university faculty (Bloomsburg University of PennsylvaniaBloomsburg University of PennsylvaniaBloomsburg University of Pennsylvania, commonly referred to as Bloomsburg, BU or Bloom, is a public university in Bloomsburg, Pennsylvania, United States...
) - Deciding where to locate offshore manufacturing plantsOffshoringOffshoring describes the relocation by a company of a business process from one country to another—typically an operational process, such as manufacturing, or supporting processes, such as accounting. Even state governments employ offshoring...
(University of CambridgeUniversity of CambridgeThe University of Cambridge is a public research university located in Cambridge, United Kingdom. It is the second-oldest university in both the United Kingdom and the English-speaking world , and the seventh-oldest globally...
) - Assessing riskRiskRisk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
in operating cross-country petroleum pipelinesPipeline transportPipeline transport is the transportation of goods through a pipe. Most commonly, liquids and gases are sent, but pneumatic tubes that transport solid capsules using compressed air are also used....
(American Society of Civil EngineersAmerican Society of Civil EngineersThe American Society of Civil Engineers is a professional body founded in 1852 to represent members of the civil engineering profession worldwide. It is the oldest national engineering society in the United States. ASCE's vision is to have engineers positioned as global leaders who strive toward...
) - Deciding how best to manage U.S. watershedsWatershed managementWatershed management is the study of the relevant characteristics of a watershed aimed at the sustainable distribution of its resources and the process of creating and implementing plans, programs, and projects to sustain and enhance watershed functions that affect the plant, animal, and human...
(U.S. Department of Agriculture)
AHP is sometimes used in designing highly specific procedures for particular situations, such as the rating of buildings by historic significance. It was recently applied to a project that uses video
Video
Video is the technology of electronically capturing, recording, processing, storing, transmitting, and reconstructing a sequence of still images representing scenes in motion.- History :...
footage to assess the condition of highways in Virginia
Virginia
The Commonwealth of Virginia , is a U.S. state on the Atlantic Coast of the Southern United States. Virginia is nicknamed the "Old Dominion" and sometimes the "Mother of Presidents" after the eight U.S. presidents born there...
. Highway engineers first used it to determine the optimum scope of the project
Project
A project in business and science is typically defined as a collaborative enterprise, frequently involving research or design, that is carefully planned to achieve a particular aim. Projects can be further defined as temporary rather than permanent social systems that are constituted by teams...
, then to justify its budget
Budget
A budget is a financial plan and a list of all planned expenses and revenues. It is a plan for saving, borrowing and spending. A budget is an important concept in microeconomics, which uses a budget line to illustrate the trade-offs between two or more goods...
to lawmakers.
Education and scholarly research
Though using the Analytic Hierarchy Process requires no specialized academic trainingTraining
The term training refers to the acquisition of knowledge, skills, and competencies as a result of the teaching of vocational or practical skills and knowledge that relate to specific useful competencies. It forms the core of apprenticeships and provides the backbone of content at institutes of...
, it is considered an important subject in many institutions of higher learning, including schools of engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and graduate schools of business
Business school
A business school is a university-level institution that confers degrees in Business Administration. It teaches topics such as accounting, administration, economics, entrepreneurship, finance, information systems, marketing, organizational behavior, public relations, strategy, human resource...
. It is a particularly important subject in the quality field, and is taught in many specialized courses including Six Sigma
Six Sigma
Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
, Lean Six Sigma
Lean Six Sigma
In recent years, some practitioners have combined Six Sigma ideas with lean manufacturing to yield a methodology named Lean Six Sigma. Lean manufacturing – addressing process flow and waste issues – and Six Sigma, with its focus on variation and design, are viewed as complementary disciplines in...
, and QFD
Quality function deployment
Quality function deployment is a “method to transform user demands into design quality, to deploy the functions forming quality, and to deploy methods for achieving the design quality into subsystems and component parts, and ultimately to specific elements of the manufacturing process.”, as...
.
The value of the AHP is recognized in developed and developing countries around the world. China is a good example — nearly a hundred Chinese universities offer courses in AHP, and many doctoral students choose AHP as the subject of their research
Research
Research can be defined as the scientific search for knowledge, or as any systematic investigation, to establish novel facts, solve new or existing problems, prove new ideas, or develop new theories, usually using a scientific method...
and dissertations. Over 900 papers have been published on the subject in China, and there is at least one Chinese scholarly journal devoted exclusively to AHP.
The International Symposium on the Analytic Hierarchy Process
International Symposium on the Analytic Hierarchy Process
The International Symposium on the Analytic Hierarchy Process is a biennial conference on multi-criteria decision analysis, particularly the analytic hierarchy process and its extension the analytic network process , both developed by Thomas L. Saaty, and the combination of these with other methods...
(ISAHP) holds biennial meetings of academics and practitioners interested in the field. A wide range of topics are covered. Those in 2005 ranged from Establishing Payment Standards for Surgical Specialists, to Strategic Technology Roadmapping, to Infrastructure Reconstruction in Devastated Countries.
At the 2007 meeting in Valparaíso, Chile, over 90 papers were presented from 19 countries, including the U.S., Germany, Japan, Chile
Chile
Chile ,officially the Republic of Chile , is a country in South America occupying a long, narrow coastal strip between the Andes mountains to the east and the Pacific Ocean to the west. It borders Peru to the north, Bolivia to the northeast, Argentina to the east, and the Drake Passage in the far...
, Malaysia, and Nepal
Nepal
Nepal , officially the Federal Democratic Republic of Nepal, is a landlocked sovereign state located in South Asia. It is located in the Himalayas and bordered to the north by the People's Republic of China, and to the south, east, and west by the Republic of India...
. A similar number of papers were presented at the 2009 symposium in Pittsburgh, Pennsylvania
Pittsburgh, Pennsylvania
Pittsburgh is the second-largest city in the US Commonwealth of Pennsylvania and the county seat of Allegheny County. Regionally, it anchors the largest urban area of Appalachia and the Ohio River Valley, and nationally, it is the 22nd-largest urban area in the United States...
, when 28 countries were represented. Subjects of the papers included Economic Stabilization in Latvia, Portfolio Selection in the Banking Sector, Wildfire Management to Help Mitigate Global Warming, and Rural Microprojects in Nepal.
Using the Analytic Hierarchy Process

The procedure for using the AHP can be summarized as:
- Model the problem as a hierarchy containing the decision goal, the alternatives for reaching it, and the criteria for evaluating the alternatives.
- Establish priorities among the elements of the hierarchy by making a series of judgments based on pairwise comparisons of the elements. For example, when comparing potential real-estate purchases, the investors might say they prefer location over price and price over timing.
- Synthesize these judgments to yield a set of overall priorities for the hierarchy. This would combine the investors' judgments about location, price and timing for properties A, B, C, and D into overall priorities for each property.
- Check the consistency of the judgments.
- Come to a final decision based on the results of this process.
These steps are more fully described below.
Model the problem as a hierarchy
The first step in the Analytic Hierarchy Process is to model the problem as a hierarchy. In doing this, participants explore the aspects of the problem at levels from general to detailed, then express it in the multileveled way that the AHP requires. As they work to build the hierarchy, they increase their understanding of the problem, of its context, and of each other's thoughts and feelings about both.Hierarchies defined
A hierarchy is a stratified system of ranking and organizing people, things, ideas, etc., where each element of the system, except for the top one, is subordinate to one or more other elements. Though the concept of hierarchy is easily grasped intuitively, it can also be described mathematically. Diagrams of hierarchies are often shaped roughly like pyramids, but other than having a single element at the top, there is nothing necessarily pyramid-shaped about a hierarchy.Human organizations are often structured as hierarchies, where the hierarchical system is used for assigning responsibilities, exercising leadership, and facilitating communication. Familiar hierarchies of "things" include a desktop computer's tower unit at the "top", with its subordinate monitor, keyboard, and mouse "below."
In the world of ideas, we use hierarchies to help us acquire detailed knowledge of complex reality: we structure the reality into its constituent parts, and these in turn into their own constituent parts, proceeding down the hierarchy as many levels as we care to. At each step, we focus on understanding a single component of the whole, temporarily disregarding the other components at this and all other levels. As we go through this process, we increase our global understanding of whatever complex reality we are studying.
Think of the hierarchy that medical students use while learning anatomy—they separately consider the musculoskeletal system (including parts and subparts like the hand and its constituent muscles and bones), the circulatory system (and its many levels and branches), the nervous system (and its numerous components and subsystems), etc., until they've covered all the systems and the important subdivisions of each. Advanced students continue the subdivision all the way to the level of the cell or molecule. In the end, the students understand the "big picture" and a considerable number of its details. Not only that, but they understand the relation of the individual parts to the whole. By working hierarchically, they've gained a comprehensive understanding of anatomy.
Similarly, when we approach a complex decision problem, we can use a hierarchy to integrate large amounts of information into our understanding of the situation. As we build this information structure, we form a better and better picture of the problem as a whole.
Hierarchies in the AHP
An AHP hierarchy is a structured means of modeling the decision at hand. It consists of an overall goal, a group of options or alternatives for reaching the goal, and a group of factors or criteria that relate the alternatives to the goal. The criteria can be further broken down into subcriteria, sub-subcriteria, and so on, in as many levels as the problem requires. A criterion may not apply uniformly, but may have graded differences like a little sweetness is enjoyable but too much sweetness can be harmful. In that case the criterion is divided into subcriteria indicating different intensities of the criterion, like: little, medium, high and these intensities are prioritized through comparisons under the parent criterion, sweetness.Published descriptions of AHP applications often include diagrams and descriptions of their hierarchies; some simple ones are shown throughout this article. More complex AHP hierarchies have been collected and reprinted in at least one book. More complex hierarchies can be found in this article's talk page.
The design of any AHP hierarchy will depend not only on the nature of the problem at hand, but also on the knowledge, judgments, values, opinions, needs, wants, etc. of the participants in the decision making process. Constructing a hierarchy typically involves significant discussion, research, and discovery by those involved. Even after its initial construction, it can be changed to accommodate newly-thought-of criteria or criteria not originally considered to be important; alternatives can also be added, deleted, or changed.
To better understand AHP hierarchies, consider a decision problem with a goal to be reached, three alternative ways of reaching the goal, and four criteria against which the alternatives need to be measured.
Such a hierarchy can be visualized as a diagram like the one immediately below, with the goal at the top, the three alternatives at the bottom, and the four criteria in between. There are useful terms for describing the parts of such diagrams: Each box is called a node. A node that is connected to one or more nodes in a level below it is called a parent node. The nodes to which it is so connected are called its children.
Applying these definitions to the diagram below, the Goal is the parent of the four Criteria, and the four Criteria are children of the Goal. Each Criterion is a parent of the three Alternatives. Note that there are only three Alternatives, but in the diagram, each of them is repeated under each of its parents.
To reduce the size of the drawing required, it is common to represent AHP hierarchies as shown in the diagram below, with only one node for each alternative, and with multiple lines connecting the alternatives and the criteria that apply to them. To avoid clutter, these lines are sometimes omitted or reduced in number. Regardless of any such simplifications in the diagram, in the actual hierarchy each alternative is connected to every one of its parent nodes.
Evaluate the hierarchy
Once the hierarchy has been constructed, the participants analyze it through a series of pairwise comparisons that derive numerical scales of measurement for the nodes. The criteria are pairwise compared against the goal for importance. The alternatives are pairwise compared against each of the criteria for preference. The comparisons are processed mathematically, and priorities are derived for each node.Consider the "Choose a Leader" example above. An important task of the decision makers is to determine the weight to be given each criterion in making the choice of a leader. Another important task is to determine the weight to be given to each candidate with regard to each of the criteria. The AHP not only lets them do that, but it lets them put a meaningful and objective numerical value on each of the four criteria.
Establish priorities
This section explains priorities, shows how they are established, and provides a simple example.Priorities defined and explained
Priorities are numbers associated with the nodes of an AHP hierarchy. They represent the relative weights of the nodes in any group.Like probabilities, priorities are absolute number
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
s between zero and one, without units or dimensions. A node with priority .200 has twice the weight in reaching the goal as one with priority .100, ten times the weight of one with priority .020, and so forth. Depending on the problem at hand, "weight" can refer to importance, or preference, or likelihood, or whatever factor is being considered by the decision makers.
Priorities are distributed over a hierarchy according to its architecture, and their values depend on the information entered by users of the process. Priorities of the Goal, the Criteria, and the Alternatives are intimately related, but need to be considered separately.
By definition, the priority of the Goal is 1.000. The priorities of the Alternatives always add up to 1.000. Things can become complicated with multiple levels of Criteria, but if there is only one level, their priorities also add to 1.000. All this is illustrated by the priorities in the example below.

The priorities shown are those that exist before any information has been entered about weights of the criteria or alternatives, so the priorities within each level are all equal. They are called the hierarchy's default priorities. If a fifth Criterion were added to this hierarchy, the default priority for each Criterion would be .200. If there were only two Alternatives, each would have a default priority of .500.
Two additional concepts apply when a hierarchy has more than one level of criteria: local priorities and global priorities. Consider the hierarchy shown below, which has several Subcriteria under each Criterion.

The rule is this: Within a hierarchy, the global priorities of child nodes always add up to the global priority of their parent. Within a group of children, the local priorities add up to 1.000.
So far, we have looked only at default priorities. As the Analytical Hierarchy Process moves forward, the priorities will change from their default values as the decision makers input information about the importance of the various nodes. They do this by making a series of pairwise comparisons.
Practical examples
Experienced practitioners know that the best way to understand the AHP is to work through cases and examples. Two detailed case studiesCase study
A case study is an intensive analysis of an individual unit stressing developmental factors in relation to context. The case study is common in social sciences and life sciences. Case studies may be descriptive or explanatory. The latter type is used to explore causation in order to find...
, specifically designed as in-depth teaching examples, are provided as appendices to this article:
- Simple step-by-step example with four Criteria and three Alternatives: Choosing a leader for an organization.
- More complex step-by-step example with ten Criteria/Subcriteria and six Alternatives: Buying a family car.
Some of the books on AHP contain practical examples of its use, though they are not typically intended to be step-by-step learning aids. One of them contains a handful of expanded examples, plus about 400 AHP hierarchies briefly described and illustrated with figures. Many examples are discussed, mostly for professional audiences, in papers published by the International Symposium on the Analytic Hierarchy Process
International Symposium on the Analytic Hierarchy Process
The International Symposium on the Analytic Hierarchy Process is a biennial conference on multi-criteria decision analysis, particularly the analytic hierarchy process and its extension the analytic network process , both developed by Thomas L. Saaty, and the combination of these with other methods...
.
Criticisms
The AHP is included in most operations researchOperations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
and management science textbooks, and is taught in numerous universities; it is used extensively in organizations that have carefully investigated its theoretical underpinnings. While the general consensus is that it is both technically valid and practically useful, the method does have its critics. Most of the criticisms involve a phenomenon called rank reversal, discussed in the following section.
Rank reversal
Decision making involves ranking alternatives in terms of criteria or attributes of those alternatives. It is an axiom of some decision theories that when new alternatives are added to a decision problem, the ranking of the old alternatives must not change — that "rank reversal" must not occur.
The reasonableness of this axiom for all applications is questionable, since there are real-world examples where adding new alternatives can change the rank of the old ones. There are also situations where it is not reasonable for the rank of existing alternatives to change when a new alternative that is not as good as any of the existing alternatives is added for consideration.
The 2000 U.S. presidential election
United States presidential election, 2000
The United States presidential election of 2000 was a contest between Republican candidate George W. Bush, then-governor of Texas and son of former president George H. W. Bush , and Democratic candidate Al Gore, then-Vice President....
is an example of a decision that can be understood as involving rank reversal. Ralph Nader
Ralph Nader
Ralph Nader is an American political activist, as well as an author, lecturer, and attorney. Areas of particular concern to Nader include consumer protection, humanitarianism, environmentalism, and democratic government....
was an 'irrelevant' alternative, in that he was dominated by both the Democrat
Democratic Party (United States)
The Democratic Party is one of two major contemporary political parties in the United States, along with the Republican Party. The party's socially liberal and progressive platform is largely considered center-left in the U.S. political spectrum. The party has the lengthiest record of continuous...
and Republican
Republican Party (United States)
The Republican Party is one of the two major contemporary political parties in the United States, along with the Democratic Party. Founded by anti-slavery expansion activists in 1854, it is often called the GOP . The party's platform generally reflects American conservatism in the U.S...
candidates. However, since he may have attracted more votes from those who would have voted Democratic rather than Republican, his presence caused the ranks to reverse. Put another way, if Nader were not in the race, it is conceivable that Al Gore
Al Gore
Albert Arnold "Al" Gore, Jr. served as the 45th Vice President of the United States , under President Bill Clinton. He was the Democratic Party's nominee for President in the 2000 U.S. presidential election....
would have won. The same could be said for the impact that Ross Perot had on George Bush's loss in 1992.
There are two schools of thought about rank reversal. One maintains that new alternatives that introduce no additional attributes should not cause rank reversal under any circumstances. The other maintains that there are some situations in which rank reversal can reasonably be expected. The original formulation of AHP allowed rank reversals. In 1993, Forman introduced a second AHP synthesis mode, called the ideal synthesis mode, to address choice situations in which the addition or removal of an 'irrelevant' alternative should not and will not cause a change in the ranks of existing alternatives. The current version of the AHP can accommodate both these schools — its Ideal Mode preserves rank, while its Distributive Mode allows the ranks to change. Either mode is selected according to the problem at hand.
Rank reversal and the AHP are extensively discussed in a 2001 paper in Operations Research, as well as a chapter entitled Rank Preservation and Reversal, in the current basic book on AHP. The latter presents published examples of rank reversal due to adding copies and near copies of an alternative, due to intransitivity of decision rules, due to adding phantom and decoy alternatives, and due to the switching phenomenon in utility functions. It also discusses the Distributive and Ideal Modes of the AHP.
See also
- Analytic Network ProcessAnalytic Network ProcessThe analytic network process is a more general form of the analytic hierarchy process used in multi-criteria decision analysis.AHP structures a decision problem into a hierarchy with a goal, decision criteria, and alternatives, while the ANP structures it as a network...
- Arrow's impossibility theoremArrow's impossibility theoremIn social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
- Decision makingDecision makingDecision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
- Decision making softwareDecision making softwareDecision-making software is a term integrating decision analysis tools to facilitate a person's decision-making process, which results in a choice of a course of action or a variant among several alternatives...
- multi-criteria decision analysisMulti-Criteria Decision AnalysisMultiple-criteria decision-making or multiple-criteria decision analysis is a sub-discipline of operations research that explicitly considers multiple criteria in decision-making environments. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria...
- Thomas L. Saaty
- Pairwise comparisonPairwise comparisonPairwise comparison generally refers to any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social...
- PreferencePreference-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
- L. L. Thurstone
- Law of comparative judgmentLaw of comparative judgmentThe law of comparative judgment was conceived by L. L. Thurstone. In modern day terminology, it is more aptly described as a model that is used to obtain measurements from any process of pairwise comparison...
Further reading
Together, these four books provide a comprehensive picture of the Analytic Hierarchy Process. Unless noted, all are by Thomas L. Saaty.- Decision Making for Leaders: The Analytical Hierarchy Process for Decisions in a Complex World (1982). Belmont, California: Wadsworth. ISBN 0-534-97959-9; Paperback, Pittsburgh: RWS. ISBN 0-9620317-0-4. "Focuses on practical application of the AHP; briefly covers theory."
- Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process (1994). Pittsburgh: RWS. ISBN 0-9620317-6-3. "A thorough exposition of the theoretical aspects of AHP."
- Principia Mathematica Decernendi: Mathematical Principles of Decision Making.... (2009). Pittsburgh: RWS. ISBN 1-888603-10-0. "Comprehensive coverage of the AHP, its successor the ANPAnalytic Network ProcessThe analytic network process is a more general form of the analytic hierarchy process used in multi-criteria decision analysis.AHP structures a decision problem into a hierarchy with a goal, decision criteria, and alternatives, while the ANP structures it as a network...
, and further developments of their underlying concepts." - The Hierarchon: A Dictionary of Hierarchies (1992), with Ernest H. Forman. Pittsburgh: RWS. ISBN 0-9620317-5-5. "Dozens of illustrations and examples of AHP hierarchies. A beginning classification of ideas relating to planning, conflict resolution, and decision making."
- International Journal of the Analytic Hierarchy Process An online journal about multi-criteria decision makingMulti-Criteria Decision AnalysisMultiple-criteria decision-making or multiple-criteria decision analysis is a sub-discipline of operations research that explicitly considers multiple criteria in decision-making environments. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria...
using the AHP.
These books also provide useful information about the AHP and its applications:
- The Logic of Priorities: Applications in Business, Energy, Health, and Transportation (1982), with Luis G. Vargas. Boston: Kluwer-Nijhoff. ISBN 0-89838-071-5 (Hardcover) ISBN 0-89838-078-2 (Paperback). Republished 1991 by RWS, ISBN 1-888603-07-0.
- Analytical Planning: The Organization of Systems (1985), with Kevin P. Kearns. Oxford: Pergamon Press. ISBN 0-08-032599-8. Republished 1991 by RWS, ISBN 1-888603-07-0.
- Conflict Resolution: The Analytic Hierarchy Process (1989), with Joyce Alexander, New York: Praeger. ISBN 0-275-93229-F
- Prediction, Projection and Forecasting: Applications of the Analytic Hierarchy Process in Economics, Finance, Politics, Games and Sports (1991), with Luis G. Vargas. Boston: Kluwer Academic. ISBN 0-7923-9104-7
- Decision Making in Economic, Social and Technological Environments (1994), with Luis G. Vargas, Pittsburgh: RWS. ISBN 0-9620317-7-1
- Models, Methods, Concepts & Applications of the Analytic Hierarchy Process (2001), with Luis G. Vargas, Boston: Kluwer Academic. ISBN 0-7923-7267-0
- Group Decision Making: Drawing Out and Reconciling Differences (2007), with Kirti Peniwati. Pittsburgh: RWS. ISBN 1-888603-08-9
External links
- AHP video. (9:17 YouTube clip) Very thorough exposition of AHP by Dr. Klaus Göpel
- Analytic Hierarchy Process (AHP) Example with Simulations using Matlab - Waqqas Farooq - AHP example for college selection using matlab.
- An illustrated guide (pdf) - Dr. Oliver Meixner University of Wien - "Analytic Hierarchy Process", a very easy to understand summary of the mathematical theory
- AHP example with Matlab implementation - AHP explanation with an example and matlab code.
- Introductory Mathematics of the Analytic Hierarchy Process - An introduction to the mathematics of the Analytic Hierarchy Process.

