Analytic torsion
Encyclopedia
In mathematics, Reidemeister torsion (or R-torsion, or Reidemeister–Franz torsion) is a topological invariant of manifold
s introduced by Kurt Reidemeister
for 3-manifold
s and generalized to higher dimension
s by and .
Analytic torsion (or Ray–Singer torsion) is an invariant of Riemannian manifold
s defined by as an analytic analogue of Reidemeister torsion. and proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
Reidemeister torsion was the first invariant in algebraic topology
that could distinguish between spaces which are homotopy equivalent but not homeomorphic, and can thus be seen as the birth of geometric topology
as a distinct field. It can be used to classify lens space
s.
Reidemeister torsion is closely related to Whitehead torsion
; see . For later work on torsion see the books , .
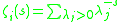
for s large, and this is extended to all complex s by analytic continuation
.
The zeta regularized determinant of the Laplacian acting on i-forms is
which is formally the product of the positive eigenvalues of the laplacian acting on i-forms.
The analytic torsion T(M,E) is defined to be
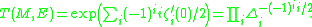
with fundamental group
π := π1(X) and U an orthogonal finite-dimensional π-representation. Suppose that
for all n. If we fix a cellular basis for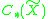
and an orthogonal R-basis for U, then 
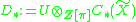is a contractible finite based free R-chain complex. Let 
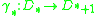be any chain contraction of D*, i.e. 
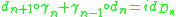for all n. We obtain an isomorphism 
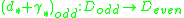with 
, 
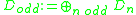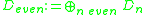. We define the Reidemeister torsion
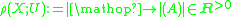
where A is the matrix of (d* + γ*)odd with respect to the given bases. The Reidemeister torsion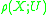
is independent of the choice of the cellular basis for 
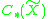, the orthogonal basis for U and the chain contraction γ*.
s in . The classification includes examples of homotopy equivalent 3-dimensional manifolds which are not homeomorphic – at the time (1935) the classification was only up to PL homeomorphism, but later showed that this was in fact a classification up to homeomorphism
.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s introduced by Kurt Reidemeister
Kurt Reidemeister
Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...
for 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s and generalized to higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s by and .
Analytic torsion (or Ray–Singer torsion) is an invariant of Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s defined by as an analytic analogue of Reidemeister torsion. and proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.
Reidemeister torsion was the first invariant in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
that could distinguish between spaces which are homotopy equivalent but not homeomorphic, and can thus be seen as the birth of geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
as a distinct field. It can be used to classify lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s.
Reidemeister torsion is closely related to Whitehead torsion
Whitehead torsion
In geometric topology, the obstruction to a homotopy equivalence f\colon X \to Y of finite CW-complexes being a simple homotopy equivalence is its Whitehead torsion \tau, which is an element in the Whitehead group Wh. These are named after the mathematician J. H. C...
; see . For later work on torsion see the books , .
Definition of analytic torsion
If M is a Riemannian manifold and E a vector bundle over M, then there is a Laplacian operator acting on the i-forms with values in E. If the eigenvalues on i-forms are λj then the zeta function ζi is defined to be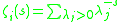for s large, and this is extended to all complex s by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
The zeta regularized determinant of the Laplacian acting on i-forms is
which is formally the product of the positive eigenvalues of the laplacian acting on i-forms.
The analytic torsion T(M,E) is defined to be
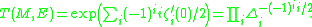
Definition of Reidemeister torsion
Let X be a finite connected CW-complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
with fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π := π1(X) and U an orthogonal finite-dimensional π-representation. Suppose that
for all n. If we fix a cellular basis for
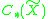and an orthogonal R-basis for U, then 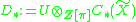is a contractible finite based free R-chain complex. Let 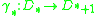be any chain contraction of D*, i.e. 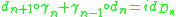for all n. We obtain an isomorphism 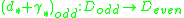with 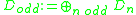, 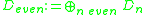. We define the Reidemeister torsion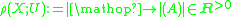where A is the matrix of (d* + γ*)odd with respect to the given bases. The Reidemeister torsion
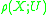is independent of the choice of the cellular basis for 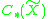, the orthogonal basis for U and the chain contraction γ*.Examples
Reidemeister torsion was first used to classify 3-dimensional lens spaceLens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s in . The classification includes examples of homotopy equivalent 3-dimensional manifolds which are not homeomorphic – at the time (1935) the classification was only up to PL homeomorphism, but later showed that this was in fact a classification up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.