Angular momentum of light
Encyclopedia
The angular momentum of light is a vector
quantity that expresses the amount of dynamical rotation present in the electromagnetic field
of the light
. Indeed, a beam of light, while traveling approximately in a straight line, can also be rotating (or “spinning”, or “twisting”) around its own axis. This rotation, not visible to the naked eye
, however can be revealed by the interaction of the light beam with matter. The total angular momentum of light (or, more generally, of the electromagnetic field
and the other force
fields) and matter is conserved in time. But there are actually two distinct forms of rotation of a light beam, one involving its polarization
and the other its wavefront
shape. These two forms of rotation are hence associated with two distinct forms of angular momentum, respectively named light spin angular momentum
(SAM) and light orbital angular momentum
(OAM).
but also momentum
, that is a characteristic property of all objects in translational motion. The existence of this momentum becomes apparent in the “radiation pressure
” phenomenon, in which a light beam transfers its momentum to an illuminated absorbing or scattering object, generating a mechanical pressure
on it in the process.
Less widely known is the fact that light may also carry angular momentum
, which is a property of all objects in rotational motion. For example, a light beam can be rotating around its own axis while it propagates forward. Again, the existence of this angular momentum can be made evident by transferring it to small absorbing or scattering particles, which are thus subject to an optical torque.
For a light beam, one can usually distinguish two “forms of rotation”, the first associated with the dynamical rotation of the electric and magnetic fields around the propagation direction, and the second with the dynamical rotation of light rays around the main beam axis. These two rotations are associated with two forms of angular momentum
, namely SAM and OAM. However this distinction becomes blurred for strongly focused or diverging beams, and in the general case only the total angular momentum of a light field can be defined. An important limiting case in which the distinction is instead clear and unambiguous is that of a “paraxial” light beam, that is a well collimated beam in which all light rays (or, more precisely, all Fourier
components of the optical field
) only form small angles with the beam axis.
For such a beam, SAM is strictly related with the optical polarization
, and in particular with the so-called circular polarization
. OAM is related with the spatial field distribution, and in particular with the wavefront
helical shape.
In addition to these two terms, if the origin of coordinates is located outside the beam axis, there is a third angular momentum
contribution obtained as the cross-product of the beam position and its total momentum
. This third term is also called “orbital”, because it depends from the spatial distribution of the field. However, since its value is dependent from the choice of the origin, it is termed “external” orbital angular momentum, as opposed to the “internal” OAM appearing for helical beams.
of an electromagnetic field
is the following one, in which there is no explicit distinction between the two forms of rotation:
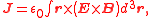
where
and 
are the electric and magnetic fields, respectively,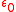 
is the vacuum permittivity and we are using SI units.
However, another expression of the angular momentum naturally arising from Noether’s theorem is the following one, in which there are two separate terms that may be associated with SAM and OAM :
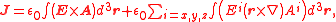
where
is the vector potential
of the magnetic field, and the i-superscripted symbols denote the cartesian components of the corresponding vectors.
These two expressions can be proved to be equivalent to each other for any electromagnetic field that vanishes fast enough outside a finite region of space. The two terms in the second expression however are not physically unambiguous, as they are not gauge-invariant. A gauge-invariant version can be obtained by replacing the vector potential A and the electric field E with their “transverse” or radiative component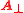
and 
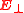, thus obtaining the following expression:
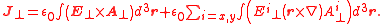
Also the latter expression has problems, however, as it can be shown that while the two terms are physically unambiguous, they are not true angular momenta, as they do not obey the correct quantum commutation rules. Their sum, that is the total angular momentum, instead does.
An equivalent but simpler expression for a monochromatic wave of frequency ω, using the complex notation for the fields, is the following :
Let us now consider the paraxial limit, with the beam axis assumed to coincide with the z axis of the coordinate system. In this limit the only significant component of the angular momentum is the z one, that is the angular momentum measuring the light beam rotation around its own axis, while the other two components are negligible.
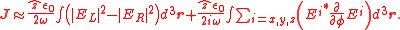
where
and 
denote the left and right circular polarization components, respectively.
In the case of transparent media, in the paraxial limit, the optical SAM is mainly exchanged with anisotropic systems, for example birefringent crystals. Indeed, thin slabs of birefringent crystals are commonly used to manipulate the light polarization. Whenever the polarization ellipticity is changed, in the process, there is an exchange of SAM between light and the crystal. If the crystal is free to rotate, it will do so. Otherwise, the SAM is finally transferred to the holder and to the Earth.
Vector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
quantity that expresses the amount of dynamical rotation present in the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
of the light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
. Indeed, a beam of light, while traveling approximately in a straight line, can also be rotating (or “spinning”, or “twisting”) around its own axis. This rotation, not visible to the naked eye
Eye
Eyes are organs that detect light and convert it into electro-chemical impulses in neurons. The simplest photoreceptors in conscious vision connect light to movement...
, however can be revealed by the interaction of the light beam with matter. The total angular momentum of light (or, more generally, of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
and the other force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
fields) and matter is conserved in time. But there are actually two distinct forms of rotation of a light beam, one involving its polarization
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
and the other its wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
shape. These two forms of rotation are hence associated with two distinct forms of angular momentum, respectively named light spin angular momentum
Light spin angular momentum
The spin angular momentum of light is the component of angular momentum of a light beam that can be associated with its circular or elliptical polarization.- Introduction :...
(SAM) and light orbital angular momentum
Light orbital angular momentum
The light orbital angular momentum is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a...
(OAM).
Introduction
It is well known that light, or more generally an electromagnetic wave, carries not only energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
but also momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, that is a characteristic property of all objects in translational motion. The existence of this momentum becomes apparent in the “radiation pressure
Radiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
” phenomenon, in which a light beam transfers its momentum to an illuminated absorbing or scattering object, generating a mechanical pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
on it in the process.
Less widely known is the fact that light may also carry angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, which is a property of all objects in rotational motion. For example, a light beam can be rotating around its own axis while it propagates forward. Again, the existence of this angular momentum can be made evident by transferring it to small absorbing or scattering particles, which are thus subject to an optical torque.
For a light beam, one can usually distinguish two “forms of rotation”, the first associated with the dynamical rotation of the electric and magnetic fields around the propagation direction, and the second with the dynamical rotation of light rays around the main beam axis. These two rotations are associated with two forms of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, namely SAM and OAM. However this distinction becomes blurred for strongly focused or diverging beams, and in the general case only the total angular momentum of a light field can be defined. An important limiting case in which the distinction is instead clear and unambiguous is that of a “paraxial” light beam, that is a well collimated beam in which all light rays (or, more precisely, all Fourier
Fourier
Fourier most commonly refers to Joseph Fourier , French mathematician and physicist, or the mathematics, physics, and engineering terms named in his honor for his work on the concepts underlying them:In mathematics:...
components of the optical field
Optical field
The optical field is a term used in physics and vector calculus to designate the electric field shown as E in the electromagnetic wave equation which can be derived from Maxwell's Equations...
) only form small angles with the beam axis.
For such a beam, SAM is strictly related with the optical polarization
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
, and in particular with the so-called circular polarization
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
. OAM is related with the spatial field distribution, and in particular with the wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
helical shape.
In addition to these two terms, if the origin of coordinates is located outside the beam axis, there is a third angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
contribution obtained as the cross-product of the beam position and its total momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. This third term is also called “orbital”, because it depends from the spatial distribution of the field. However, since its value is dependent from the choice of the origin, it is termed “external” orbital angular momentum, as opposed to the “internal” OAM appearing for helical beams.
Mathematical expressions for the angular momentum of light
One commonly used expression for the total angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
of an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
is the following one, in which there is no explicit distinction between the two forms of rotation:
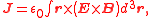
where
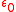and are the electric and magnetic fields, respectively, is the vacuum permittivity and we are using SI units.However, another expression of the angular momentum naturally arising from Noether’s theorem is the following one, in which there are two separate terms that may be associated with SAM and OAM :
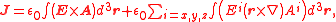
where
is the vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
of the magnetic field, and the i-superscripted symbols denote the cartesian components of the corresponding vectors.
These two expressions can be proved to be equivalent to each other for any electromagnetic field that vanishes fast enough outside a finite region of space. The two terms in the second expression however are not physically unambiguous, as they are not gauge-invariant. A gauge-invariant version can be obtained by replacing the vector potential A and the electric field E with their “transverse” or radiative component
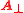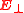and , thus obtaining the following expression: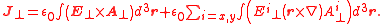Also the latter expression has problems, however, as it can be shown that while the two terms are physically unambiguous, they are not true angular momenta, as they do not obey the correct quantum commutation rules. Their sum, that is the total angular momentum, instead does.
An equivalent but simpler expression for a monochromatic wave of frequency ω, using the complex notation for the fields, is the following :
Let us now consider the paraxial limit, with the beam axis assumed to coincide with the z axis of the coordinate system. In this limit the only significant component of the angular momentum is the z one, that is the angular momentum measuring the light beam rotation around its own axis, while the other two components are negligible.
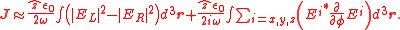
where
and denote the left and right circular polarization components, respectively.Exchange of spin and orbital angular momentum with matter
When a light beam carrying nonzero angular momentum impinges on an absorbing particle, its angular momentum can be transferred on the particle, thus setting it in rotational motion. This occurs both with SAM and OAM. However, if the particle is not at the beam center the two angular momenta will give rise to different kinds of rotation of the particle. SAM will give rise to a rotation of the particle around its own center, i.e., to a particle spinning. OAM, instead, will generate a revolution of the particle around the beam axis. These phenomena are schematically illustrated in the figure.In the case of transparent media, in the paraxial limit, the optical SAM is mainly exchanged with anisotropic systems, for example birefringent crystals. Indeed, thin slabs of birefringent crystals are commonly used to manipulate the light polarization. Whenever the polarization ellipticity is changed, in the process, there is an exchange of SAM between light and the crystal. If the crystal is free to rotate, it will do so. Otherwise, the SAM is finally transferred to the holder and to the Earth.
Spiral Phase Plate (SPP)
In the paraxial limit, the OAM of a light beam can be exchanged with material media that have a transverse spatial inhomogeneity. For example, a light beam can acquire OAM by crossing a spiral phase plate, with a inhomogeneous thickness (see figure).Pitch-Fork Hologram
A more convenient approach for generating OAM is based on using diffraction on a fork-like or pitchfork hologram (see figure). Holograms can be also generated dynamically under the control of a computer by using a spatial light modulator, or SLM.Q-Plate
Another method for generating OAM is based on the SAM-OAM coupling that may occur in a medium which is both anisotropic and inhomogeneous. In particular, the so-called q-plate is a device, currently realized using liquid crystals, polymers or sub-wavelength gratings, which can generate OAM by exploiting a SAM sign-change. In this case, the OAM sign is controlled by the input polarization.Cylindrical Mode Converters
OAM can also be generated by converting Hermite-Gaussian beams into the Laguerre-Gaussian ones by using an astigmatic system with two well-aligned cylindrical lenses placed at a specific distance (see figure) in order to introduce a well-defined relative phase between horizontal and vertical Hermite-Gauss beams.Possible applications of the orbital angular momentum of light
The applications of the spin angular momentum of light are undistinguishable from the innumerable applications of the light polarization and will not be discussed here. The possible applications of the orbital angular momentum of light are instead currently the subject of research. In particular, the following applications have been already demonstrated in research laboratories, although they have not yet reached the stage of commercialization:- Orientational manipulation of particles or particle aggregates in optical tweezers
- High-bandwidth information encoding in free-space optical communication
- Higher-dimensional quantum information encoding, for possible future quantum cryptography or quantum computation applications
- Sensitive optical detection