In mathematics and theoretical physics

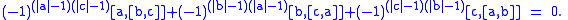
Theoretical physics

Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...

, a Gerstenhaber algebra (sometimes called an antibracket algebra or braid algebra) is an algebraic structure

Algebraic structure

In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...

 discovered by Murray Gerstenhaber

Murray Gerstenhaber

Murray Gerstenhaber is an American mathematician, professor of mathematics at the University of Pennsylvania, best known for his contributions to theoretical physics with his discovery of Gerstenhaber algebra.- About :...

 (1963) that combines the structures of a supercommutative ring and a graded Lie superalgebra. It is used in the Batalin–Vilkovisky formalism.

Definition

A Gerstenhaber algebra is a differential graded commutative algebra

Commutative algebra

Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...

 with a Lie bracket

Lie bracket

Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...

 of degree -1 satisfying the Poisson identity. Everything is understood to satisfy the usual superalgebra

Superalgebra

In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....

 sign conventions. More precisely, the algebra has two products, one written as ordinary multiplication and one written as [,], and a Z-grading called degree (in theoretical physics sometimes called ghost number). The degree of an element a is denoted by |a|. These satisfy the identities

• |ab| = |a| + |b| (The product has degree 0)
• |[a,b]| = |a| + |b| - 1 (The Lie bracket has degree -1)
• (ab)c = a(bc) (The product is associative)
• ab = (−1)^|a||b|ba (The product is (super) commutative)
• [a,bc] = [a,b]c + (−1)^(|a|-1)|b|b[a,c] (Poisson identity)
• [a,b] = −(−1)^{(|a|-1)(|b|-1)} [b,a] (Antisymmetry of Lie bracket)
• [a,[b,c]] = a  (The Jacobi identity for the Lie bracket)

Gerstenhaber algebras differ from Poisson superalgebra

Poisson superalgebra

In mathematics, a Poisson superalgebra is a Z2-graded generalization of a Poisson algebra. Specifically, a Poisson superalgebra is an superalgebra A with a Lie superbracket[\cdot,\cdot] : A\otimes A\to A...

s in that the Lie bracket has degree -1 rather than degree 0. The Jacobi identity may also be expressed in a symmetrical form

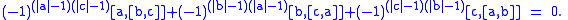
Examples

• Gerstenhaber showed that the Hochschild cohomology H^*(A,A) of a graded algebra A is a Gerstenhaber algebra.
• A Batalin–Vilkovisky algebra has an underlying Gerstenhaber algebra if one forgets its second order Δ operator.
• The exterior algebra
  Exterior algebra
  In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
  
   of a Lie algebra
  Lie algebra
  In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
  
   is a Gerstenhaber algebra.
• The differential forms on a Poisson manifold
  Poisson manifold
  In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
  
   form a Gerstenhaber algebra.
• The multivector fields on a manifold
  Manifold
  In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
  
   form a Gerstenhaber algebra using the Schouten–Nijenhuis bracket