
Poisson superalgebra
Encyclopedia
In mathematics
, a Poisson superalgebra is a Z2-graded
generalization of a Poisson algebra
. Specifically, a Poisson superalgebra is an (associative) superalgebra
A with a Lie superbracket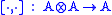
such that (A, [·,·]) is a Lie superalgebra
and the operator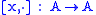
is a superderivation of A: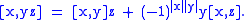
A supercommutative Poisson algebra is one for which the (associative) product is supercommutative
.
This is one possible way of "super"izing the Poisson algebra. This gives the classical dynamics of fermion fields and classical spin-1/2 particles. The other is to define an antibracket algebra
instead. This is used in the BRST
and Batalin-Vilkovisky formalism.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Poisson superalgebra is a Z2-graded
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
generalization of a Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
. Specifically, a Poisson superalgebra is an (associative) superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
A with a Lie superbracket
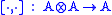
such that (A, [·,·]) is a Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
and the operator
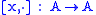
is a superderivation of A:
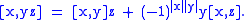
A supercommutative Poisson algebra is one for which the (associative) product is supercommutative
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
.
This is one possible way of "super"izing the Poisson algebra. This gives the classical dynamics of fermion fields and classical spin-1/2 particles. The other is to define an antibracket algebra
Antibracket algebra
In mathematics and theoretical physics, a Gerstenhaber algebra is an algebraic structure discovered by Murray Gerstenhaber that combines the structures of a supercommutative ring and a graded Lie superalgebra...
instead. This is used in the BRST
BRST
BRST may refer to:* BRST formalism and quantization in Yang-Mills theories* Big Red Switch Time , computer jargon for switching your computer off, when all other options for a more elegant shutdown have been exhausted...
and Batalin-Vilkovisky formalism.
Examples
- If A is any associative Z2 graded algebra, then, defining a new product [.,.] (which is called the super-commutator) by [x,y]:=xy-(-1)|x||y|yx for any pure graded x, y turns A into a Poisson superalgebra.

