
Antimetric (electrical networks)
Encyclopedia
An antimetric electrical network is one that exhibits anti-symmetrical
electrical properties. The term is often encountered in filter theory, but it applies to general electrical network analysis
. Antimetric is the diametrical opposite of symmetric; it does not merely mean "asymmtetric" (i.e., "lacking symmetry").
when correctly terminated. A symmetric network will have the two equal impedances, Zi1 and Zi2. For an antimetric network, the two impedances must be the dual of each other with respect to some nominal impedance R0. That is,
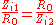
which is well-defined because R0 ≠ 0 and Zi2 ≠ 0. Hence,
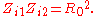
It is necessary for antimetry that the terminating impedances are also the dual of each other, but in many practical cases the two terminating impedances are resistors and are both equal to the nominal impedance R0. Hence, they are both symmetric and antimetric at the same time.
Other network parameters may also be referred to as antimetric. For instance, for a two-port network described by scattering parameters
(S-parameters),

if the network is symmetric, and
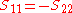
if the network is antimetric.
symmetric and antimetric, respectively. That is, the physical arrangement of their components and values are symmetric or antimetric as in the ladder example above. However, it is not a necessary condition for electrical antimetry. For example, if the example networks from the preceding section have an additional T-section added to the left-hand side, then the networks remain topologically symmetric and antimetric. However, the network resulting from the application of Bartlett's bisection theorem
applied to the first T-section in each network are neither physically symmetric nor antimetric but retain their electrical symmetric (in the first case) and antimetric (in the second case) properties.
motion and normal stress, and antimetric forces produce rotation
al motion and shear stress
. Any asymmetric pair of forces can be expressed as a linear combination of a symmetric and an antimetric pair.
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
electrical properties. The term is often encountered in filter theory, but it applies to general electrical network analysis
Network analysis (electrical circuits)
A network, in the context of electronics, is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, every component in the network. There are a number of different techniques for achieving this...
. Antimetric is the diametrical opposite of symmetric; it does not merely mean "asymmtetric" (i.e., "lacking symmetry").
Definition
References to symmetry and antimetry of a network usually refer to the input impedances of a two-port networkTwo-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
when correctly terminated. A symmetric network will have the two equal impedances, Zi1 and Zi2. For an antimetric network, the two impedances must be the dual of each other with respect to some nominal impedance R0. That is,
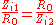
which is well-defined because R0 ≠ 0 and Zi2 ≠ 0. Hence,
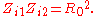
It is necessary for antimetry that the terminating impedances are also the dual of each other, but in many practical cases the two terminating impedances are resistors and are both equal to the nominal impedance R0. Hence, they are both symmetric and antimetric at the same time.
Other network parameters may also be referred to as antimetric. For instance, for a two-port network described by scattering parameters
Scattering parameters
Scattering parameters or S-parameters describe the electrical behavior of linear electrical networks when undergoing various steady state stimuli by electrical signals....
(S-parameters),

if the network is symmetric, and
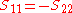
if the network is antimetric.
Physical and electrical antimetry
Symmetric and antimetric networks are often also topologicallyTopology (electronics)
The topology of an electronic circuit is the form taken by the network of interconnections of the circuit components. Different specific values or ratings of the components are regarded as being the same topology....
symmetric and antimetric, respectively. That is, the physical arrangement of their components and values are symmetric or antimetric as in the ladder example above. However, it is not a necessary condition for electrical antimetry. For example, if the example networks from the preceding section have an additional T-section added to the left-hand side, then the networks remain topologically symmetric and antimetric. However, the network resulting from the application of Bartlett's bisection theorem
Bartlett's bisection theorem
Bartlett's Bisection Theorem is an electrical theorem in network analysis due to Albert Charles Bartlett. The theorem shows that any symmetrical two-port network can be transformed into a lattice network...
applied to the first T-section in each network are neither physically symmetric nor antimetric but retain their electrical symmetric (in the first case) and antimetric (in the second case) properties.
Mechanics
Antimetry appears in mechanics as a property of forces, motions, and oscillations. Symmetric forces produce translationalTranslation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
motion and normal stress, and antimetric forces produce rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
al motion and shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
. Any asymmetric pair of forces can be expressed as a linear combination of a symmetric and an antimetric pair.

