
Area theorem (conformal mapping)
Encyclopedia
In the mathematical
theory of conformal mappings, the area theorem
gives an inequality satisfied by
the power series coefficient
s of certain conformal mappings.
The theorem is called by that name, not because of its implications, but rather because the proof uses
the notion of area
.
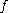 is analytic
is analytic
and injective
in the punctured
open
unit disk
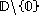 and has the power series representation
and has the power series representation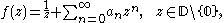
then the coefficients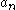 satisfy
satisfy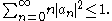
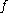 .
.
Define for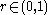
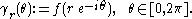
Then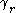 is a simple closed curve in the plane.
is a simple closed curve in the plane.
Let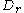 denote the unique bounded connected component of
denote the unique bounded connected component of
 . The existence and
. The existence and
uniqueness of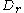 follows from Jordan's curve theorem
follows from Jordan's curve theorem
.
If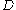 is a domain in the plane whose boundary
is a domain in the plane whose boundary
is a smooth simple closed curve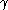 ,
,
then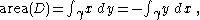
provided that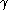 is positively oriented
is positively oriented
around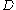 .
.
This follows easily, for example, from Green's theorem.
As we will soon see,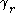 is positively oriented around
is positively oriented around
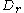 (and that is the reason for the minus sign in the
(and that is the reason for the minus sign in the
definition of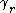 ). After applying the chain rule
). After applying the chain rule
and the formula for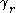 , the above expressions for
, the above expressions for
the area give
Therefore, the area of also equals to the average of the two expressions on the right
also equals to the average of the two expressions on the right
hand side. After simplification, this yields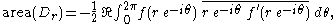
where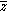 denotes complex conjugation. We set
denotes complex conjugation. We set  and use the power series
and use the power series
expansion for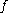 , to get
, to get
(Since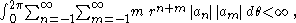 the rearrangement of the terms is justified.)
the rearrangement of the terms is justified.)
Now note that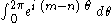 is
is 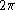 if
if 
and is zero otherwise. Therefore, we get
The area of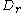 is clearly positive. Therefore, the right hand side
is clearly positive. Therefore, the right hand side
is positive. Since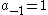 , by letting
, by letting  , the
, the
theorem now follows.
It only remains to justify the claim that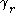 is positively oriented
is positively oriented
around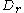 . Let
. Let 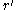 satisfy
satisfy 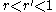 , and set
, and set
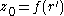 , say. For very small
, say. For very small 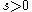 , we may write the
, we may write the
expression for the winding number
of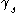 around
around 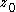 ,
,
and verify that it is equal to . Since,
. Since, 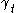 does
does
not pass through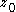 when
when 
(as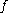 is injective), the invariance
is injective), the invariance
of the winding number under homotopy in the complement of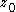
implies that the winding number of
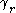 around
around 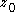 is also
is also 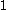 .
.
This implies that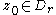 and that
and that 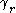
is positively oriented around , as required.
, as required.
mappings were of considerable interest to mathematicians prior to
the solution of the Bieberbach conjecture. The area theorem
is a central tool in this context. Moreover, the area theorem is often
used in order to prove the Koebe 1/4 theorem
, which is very
useful in the study of the geometry of conformal mappings.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of conformal mappings, the area theorem
gives an inequality satisfied by
the power series coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of certain conformal mappings.
The theorem is called by that name, not because of its implications, but rather because the proof uses
the notion of area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
.
Statement
Suppose that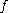 is analytic
is analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
and injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
in the punctured
open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
unit disk
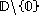 and has the power series representation
and has the power series representation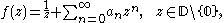
then the coefficients
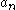 satisfy
satisfy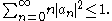
Proof
The idea of the proof is to look at the area uncovered by the image of .
.Define for
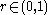
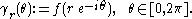
Then
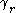 is a simple closed curve in the plane.
is a simple closed curve in the plane.Let
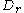 denote the unique bounded connected component of
denote the unique bounded connected component of . The existence and
. The existence anduniqueness of
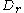 follows from Jordan's curve theorem
follows from Jordan's curve theoremJordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
.
If
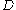 is a domain in the plane whose boundary
is a domain in the plane whose boundaryis a smooth simple closed curve
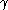 ,
,then
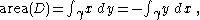
provided that
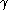 is positively oriented
is positively orientedaround
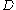 .
.This follows easily, for example, from Green's theorem.
As we will soon see,
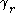 is positively oriented around
is positively oriented around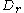 (and that is the reason for the minus sign in the
(and that is the reason for the minus sign in thedefinition of
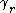 ). After applying the chain rule
). After applying the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and the formula for
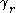 , the above expressions for
, the above expressions forthe area give

Therefore, the area of
 also equals to the average of the two expressions on the right
also equals to the average of the two expressions on the righthand side. After simplification, this yields
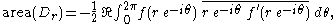
where
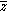 denotes complex conjugation. We set
denotes complex conjugation. We set  and use the power series
and use the power seriesexpansion for
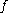 , to get
, to get
(Since
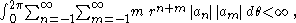 the rearrangement of the terms is justified.)
the rearrangement of the terms is justified.)Now note that
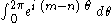 is
is 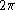 if
if 
and is zero otherwise. Therefore, we get

The area of
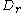 is clearly positive. Therefore, the right hand side
is clearly positive. Therefore, the right hand sideis positive. Since
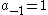 , by letting
, by letting  , the
, thetheorem now follows.
It only remains to justify the claim that
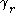 is positively oriented
is positively orientedaround
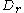 . Let
. Let 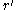 satisfy
satisfy 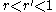 , and set
, and set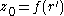 , say. For very small
, say. For very small 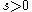 , we may write the
, we may write theexpression for the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of
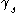 around
around 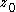 ,
,and verify that it is equal to
 . Since,
. Since, 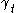 does
doesnot pass through
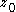 when
when 
(as
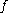 is injective), the invariance
is injective), the invarianceof the winding number under homotopy in the complement of
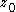
implies that the winding number of
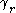 around
around 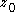 is also
is also 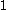 .
.This implies that
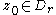 and that
and that 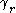
is positively oriented around
 , as required.
, as required.Uses
The inequalities satisfied by power series coefficients of conformalmappings were of considerable interest to mathematicians prior to
the solution of the Bieberbach conjecture. The area theorem
is a central tool in this context. Moreover, the area theorem is often
used in order to prove the Koebe 1/4 theorem
Koebe 1/4 theorem
In complex analysis, a branch of mathematics, the Koebe 1/4 theorem states that the image of an injective analytic function f:\mathbb D\to\mathbb C from the unit disk \mathbb D onto a subset of the complex plane contains the disk whose center is f\, and whose radius is |f\,'|/4. The theorem is...
, which is very
useful in the study of the geometry of conformal mappings.

