
Aronszajn tree
Encyclopedia
In set theory
, an Aronszajn tree is an uncountable tree
with no uncountable branches and no uncountable levels. For example, every Suslin tree
is an Aronszajn tree. More generally, for a cardinal κ, a κ-Aronszajn tree is a tree of height κ such that all levels have size less than κ and all branches have height less than κ (so Aronszajn trees are the same as -Aronszajn trees). They are named for Nachman Aronszajn, who constructed an Aronszajn tree in 1934.
-Aronszajn trees). They are named for Nachman Aronszajn, who constructed an Aronszajn tree in 1934.
A cardinal κ for which no κ-Aronszajn trees exist is said to have the tree property.
(Sometimes the condition that κ is regular and uncountable is included.)
states that -Aronszajn trees do not exist.
-Aronszajn trees do not exist.
The existence of Aronszajn trees (= -Aronszajn trees) was proven by Nachman Aronszajn, and implies that the analogue of König's lemma
-Aronszajn trees) was proven by Nachman Aronszajn, and implies that the analogue of König's lemma
does not hold for uncountable trees.
The existence of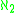 -Aronszajn trees is undecidable (assuming a certain large cardinal axiom): more precisely, the continuum hypothesis
-Aronszajn trees is undecidable (assuming a certain large cardinal axiom): more precisely, the continuum hypothesis
implies the existence of an -Aronszajn tree, and Mitchell and Silver showed that it is consistent (relative to the existence of a weakly compact cardinal
-Aronszajn tree, and Mitchell and Silver showed that it is consistent (relative to the existence of a weakly compact cardinal
) that no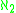 -Aronszajn trees exist.
-Aronszajn trees exist.
Jensen proved that V=L implies that there is a κ-Aronszajn tree (in fact a κ-Suslin tree) for every infinite successor cardinal κ.
showed (using a large cardinal axiom) that it is consistent that no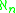 -Aronszajn trees exist for any finite n other than 1.
-Aronszajn trees exist for any finite n other than 1.
If κ is weakly compact then no κ-Aronszajn trees exist. Conversely if κ is inaccessible and no κ-Aronszajn trees exist then κ is weakly compact.
f(x)<f(y) whenever x<y. Martin's axiom
MA(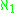 ) implies that all Aronszajn trees are special. The stronger proper forcing axiom
) implies that all Aronszajn trees are special. The stronger proper forcing axiom
implies the stronger statement that for any two Aronszajn trees there is a club set
of levels such that the restrictions of the trees to this set of levels are isomorphic, which says that in some sense any two Aronszajn trees are essentially isomorphic. On the other hand, it is consistent that non-special Aronszajn trees exist, and this is also consistent with the generalized continuum hypothesis and with the Suslin hypothesis .
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an Aronszajn tree is an uncountable tree
Tree (set theory)
In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
with no uncountable branches and no uncountable levels. For example, every Suslin tree
Suslin tree
In mathematics, a Suslin tree is a tree of height ω1 such thatevery branch and every antichain is at most countable. Every Suslin tree is an Aronszajn tree....
is an Aronszajn tree. More generally, for a cardinal κ, a κ-Aronszajn tree is a tree of height κ such that all levels have size less than κ and all branches have height less than κ (so Aronszajn trees are the same as
 -Aronszajn trees). They are named for Nachman Aronszajn, who constructed an Aronszajn tree in 1934.
-Aronszajn trees). They are named for Nachman Aronszajn, who constructed an Aronszajn tree in 1934.A cardinal κ for which no κ-Aronszajn trees exist is said to have the tree property.
(Sometimes the condition that κ is regular and uncountable is included.)
Existence of κ-Aronszajn trees
König's lemmaKönig's lemma
König's lemma or König's infinity lemma is a theorem in graph theory due to Dénes Kőnig . It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic,...
states that
 -Aronszajn trees do not exist.
-Aronszajn trees do not exist.The existence of Aronszajn trees (=
 -Aronszajn trees) was proven by Nachman Aronszajn, and implies that the analogue of König's lemma
-Aronszajn trees) was proven by Nachman Aronszajn, and implies that the analogue of König's lemmaKönig's lemma
König's lemma or König's infinity lemma is a theorem in graph theory due to Dénes Kőnig . It gives a sufficient condition for an infinite graph to have an infinitely long path. The computability aspects of this theorem have been thoroughly investigated by researchers in mathematical logic,...
does not hold for uncountable trees.
The existence of
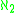 -Aronszajn trees is undecidable (assuming a certain large cardinal axiom): more precisely, the continuum hypothesis
-Aronszajn trees is undecidable (assuming a certain large cardinal axiom): more precisely, the continuum hypothesisContinuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
implies the existence of an
 -Aronszajn tree, and Mitchell and Silver showed that it is consistent (relative to the existence of a weakly compact cardinal
-Aronszajn tree, and Mitchell and Silver showed that it is consistent (relative to the existence of a weakly compact cardinalWeakly compact cardinal
In mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
) that no
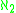 -Aronszajn trees exist.
-Aronszajn trees exist.Jensen proved that V=L implies that there is a κ-Aronszajn tree (in fact a κ-Suslin tree) for every infinite successor cardinal κ.
showed (using a large cardinal axiom) that it is consistent that no
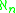 -Aronszajn trees exist for any finite n other than 1.
-Aronszajn trees exist for any finite n other than 1.If κ is weakly compact then no κ-Aronszajn trees exist. Conversely if κ is inaccessible and no κ-Aronszajn trees exist then κ is weakly compact.
Special Aronszajn trees
An Aronszajn tree is called special if there is a function f from the tree to the rationals so thatf(x)<f(y) whenever x<y. Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
MA(
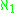 ) implies that all Aronszajn trees are special. The stronger proper forcing axiom
) implies that all Aronszajn trees are special. The stronger proper forcing axiomProper Forcing Axiom
In the mathematical field of set theory, the proper forcing axiom is a significant strengthening of Martin's axiom, where forcings with the countable chain condition are replaced by proper forcings.- Statement :...
implies the stronger statement that for any two Aronszajn trees there is a club set
Club set
In mathematics, particularly in mathematical logic and set theory, a club set is a subset of a limit ordinal which is closed under the order topology, and is unbounded relative to the limit ordinal...
of levels such that the restrictions of the trees to this set of levels are isomorphic, which says that in some sense any two Aronszajn trees are essentially isomorphic. On the other hand, it is consistent that non-special Aronszajn trees exist, and this is also consistent with the generalized continuum hypothesis and with the Suslin hypothesis .

