
Autocorrelation matrix
Encyclopedia
The autocorrelation matrix is used in various digital signal processing algorithms. It consists of elements of the discrete autocorrelation function, 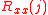 arranged in the following manner:
arranged in the following manner:

This is clearly a Hermitian matrix and a Toeplitz matrix
. Furthermore, if is a real valued function, then it is a circulant matrix
is a real valued function, then it is a circulant matrix
since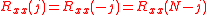 . Finally if
. Finally if  is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.
is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.
The autocovariance matrix is related to the autocorrelation matrix as follows:
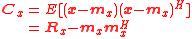
Where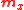 is a vector giving the mean of signal
is a vector giving the mean of signal  at each index of time.
at each index of time.
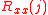 arranged in the following manner:
arranged in the following manner:
This is clearly a Hermitian matrix and a Toeplitz matrix
Toeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
. Furthermore, if
 is a real valued function, then it is a circulant matrix
is a real valued function, then it is a circulant matrixCirculant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
since
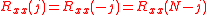 . Finally if
. Finally if  is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.
is wide-sense stationary then its autocorrelation matrix will be nonnegative definite.The autocovariance matrix is related to the autocorrelation matrix as follows:
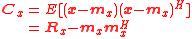
Where
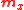 is a vector giving the mean of signal
is a vector giving the mean of signal  at each index of time.
at each index of time.

