Background field method
Encyclopedia
In theoretical physics
, background field method is a useful procedure to calculate the effective action
of a quantum field theory
by expanding a quantum field around a classical "background" value B:
After this is done, the Green's functions are evaluated as a function of the background. This approach has the advantage that the gauge invariance is manifestly preserved if the approach is applied to gauge theory
.
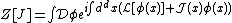
where J(x) is a source,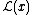
is the Lagrangian density of the system, d is the number of dimensions and φ(x) is a field.
In the background field method, one starts by splitting this field into a classical background field B(x) and a field η(x) containing additional quantum fluctuations: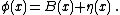
Typically, B(x) will be a solution of the classical equations of motion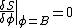
where S is the action, i.e. the space integral of the Lagrangian density. Fields obeying these equations typically yield the greatest contribution in a path integral, so it is natural to expand around them. Switching on a source J(x) will change the equations into δS/δφ|φ = B + J = 0.
Then the action is expanded around the background B(x):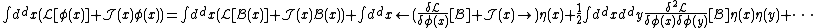
The second term in this expansion is zero by the equations of motion. The first term does not depend on any fluctuating fields, so that it can be brought out of the path integral. The result is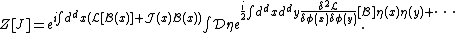
The path integral which now remains is (neglecting the corrections in the dots) of Gaussian form and can be integrated exactly: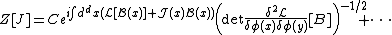
where "det" signifies a functional determinant
and C is a constant. The power of minus one half will naturally be plus one for Grassmann fields
.
The above derivation gives the Gaussian approximation to the functional integral. Corrections to this can be computed, producing a diagrammatic expansion.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, background field method is a useful procedure to calculate the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
by expanding a quantum field around a classical "background" value B:
-
.
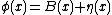After this is done, the Green's functions are evaluated as a function of the background. This approach has the advantage that the gauge invariance is manifestly preserved if the approach is applied to gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
Method
We typically want to calculate expressions like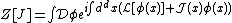where J(x) is a source,
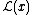is the Lagrangian density of the system, d is the number of dimensions and φ(x) is a field.In the background field method, one starts by splitting this field into a classical background field B(x) and a field η(x) containing additional quantum fluctuations:
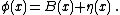
Typically, B(x) will be a solution of the classical equations of motion
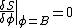
where S is the action, i.e. the space integral of the Lagrangian density. Fields obeying these equations typically yield the greatest contribution in a path integral, so it is natural to expand around them. Switching on a source J(x) will change the equations into δS/δφ|φ = B + J = 0.
Then the action is expanded around the background B(x):
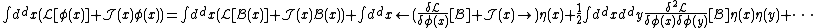
The second term in this expansion is zero by the equations of motion. The first term does not depend on any fluctuating fields, so that it can be brought out of the path integral. The result is
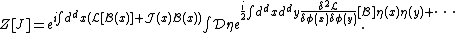
The path integral which now remains is (neglecting the corrections in the dots) of Gaussian form and can be integrated exactly:
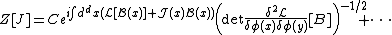
where "det" signifies a functional determinant
Functional determinant
In mathematics, if S is a linear operator mapping a function space V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant. The corresponding quantity det is called the functional determinant of S.There are several formulas for the functional...
and C is a constant. The power of minus one half will naturally be plus one for Grassmann fields
Grassmann number
In mathematical physics, a Grassmann number, named after Hermann Grassmann, is a mathematical construction which allows a path integral representation for Fermionic fields...
.
The above derivation gives the Gaussian approximation to the functional integral. Corrections to this can be computed, producing a diagrammatic expansion.