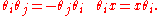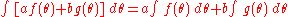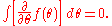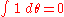Grassmann number
Encyclopedia
In mathematical physics
, a Grassmann number, named after Hermann Grassmann
, (also called an anticommuting number or anticommuting c-number
) is a mathematical construction which allows a path integral representation
for Fermionic field
s. A collection of Grassmann variables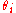
are independent elements of an algebra which contains the real numbers that anticommute with each other but commute with ordinary numbers 
:
In particular, the square of the generators vanish:
In order to reproduce the path integral for a Fermi field, the definition of Grassmann integration needs to have the following properties:
This results in the following rules for the integration of a Grassmann quantity:
Thus we conclude that the operations of integration and differentiation of a Grassmann number are identical.
In the path integral formulation
of quantum field theory
the following Gaussian integral
of Grassmann quantities is needed for fermionic anticommuting fields:
with A being an N × N matrix.
The algebra
generated by a set of Grassmann numbers is known as a Grassmann algebra. The Grassmann algebra generated by n linearly independent Grassmann numbers has dimension 2n.
Grassmann algebras are the prototypical examples of supercommutative algebra
s. These are algebras with a decomposition into even and odd variables which satisfy a graded version of commutativity
(in particular, odd elements anticommute).
of the vector space
spanned
by the generators. The exterior algebra is defined independent of a choice of basis.
. Consider, for example, the Grassmann algebra generated by two Grassmann numbers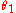
and 
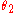. These Grassmann numbers can be represented by 4×4 matrices:
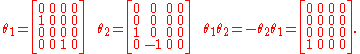
In general, a Grassmann algebra on n generators can be represented by 2n × 2n square matrices. Physically, these matrices can be thought of as raising operators acting on a Hilbert space
of n identical fermion
s in the occupation number basis. Since the occupation number for each fermion is 0 or 1, there are 2n possible basis states. Mathematically, these matrices can be interpreted as the linear operators corresponding to left exterior multiplication on the Grassmann algebra itself.
, Grassmann numbers are the "classical analogues" of anticommuting
operators. They are used to define the path integral
s of fermionic field
s. To this end it is necessary to define integrals over Grassmann variables, known as Berezin integral
s.
Grassmann numbers are also important for the definition of supermanifold
s (or superspace
) where they serve as "anticommuting coordinates".
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, a Grassmann number, named after Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
, (also called an anticommuting number or anticommuting c-number
C-number
The term c-number is an old nomenclature used by Paul Dirac which refers to real and complex numbers. It is used to distinguish from operators in quantum mechanics....
) is a mathematical construction which allows a path integral representation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
for Fermionic field
Fermionic field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi-Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields....
s. A collection of Grassmann variables
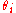are independent elements of an algebra which contains the real numbers that anticommute with each other but commute with ordinary numbers :
In particular, the square of the generators vanish:
-
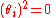, since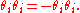 
In order to reproduce the path integral for a Fermi field, the definition of Grassmann integration needs to have the following properties:
- linearity
- partial integration formula
This results in the following rules for the integration of a Grassmann quantity:
Thus we conclude that the operations of integration and differentiation of a Grassmann number are identical.
In the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
the following Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
of Grassmann quantities is needed for fermionic anticommuting fields:
with A being an N × N matrix.
The algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
generated by a set of Grassmann numbers is known as a Grassmann algebra. The Grassmann algebra generated by n linearly independent Grassmann numbers has dimension 2n.
Grassmann algebras are the prototypical examples of supercommutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
s. These are algebras with a decomposition into even and odd variables which satisfy a graded version of commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
(in particular, odd elements anticommute).
Exterior algebra
The Grassmann algebra is the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
spanned
by the generators. The exterior algebra is defined independent of a choice of basis.
Matrix representations
Grassmann numbers can always be represented by matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Consider, for example, the Grassmann algebra generated by two Grassmann numbers
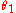and 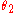. These Grassmann numbers can be represented by 4×4 matrices: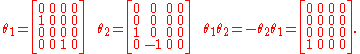In general, a Grassmann algebra on n generators can be represented by 2n × 2n square matrices. Physically, these matrices can be thought of as raising operators acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of n identical fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s in the occupation number basis. Since the occupation number for each fermion is 0 or 1, there are 2n possible basis states. Mathematically, these matrices can be interpreted as the linear operators corresponding to left exterior multiplication on the Grassmann algebra itself.
Applications
In quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, Grassmann numbers are the "classical analogues" of anticommuting
operators. They are used to define the path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
s of fermionic field
Fermionic field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi-Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields....
s. To this end it is necessary to define integrals over Grassmann variables, known as Berezin integral
Berezin integral
In mathematical physics, a Grassmann integral, or, more correctly, Berezin integral, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a...
s.
Grassmann numbers are also important for the definition of supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
s (or superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
) where they serve as "anticommuting coordinates".