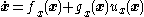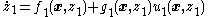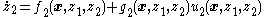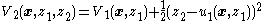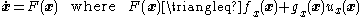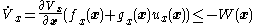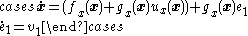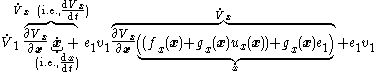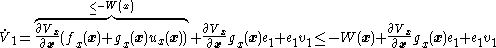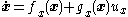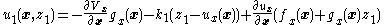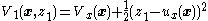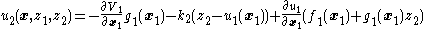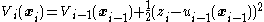Backstepping
Encyclopedia
In control theory
, backstepping is a technique developed circa
1990 by Petar V. Kokotovic
and others for designing stabilizing
controls for a special class of nonlinear dynamical system
s. These systems are built from subsystems that radiate out from an irreducible subsystem that can be stabilized using some other method. Because of this recursive
structure, the designer can start the design process at the known-stable system and "back out" new controllers that progressively stabilize each outer subsystem. The process terminates when the final external control is reached. Hence, this process is known as backstepping.
The backstepping approach provides a recursive
method for stabilizing
the origin
of a system in strict-feedback form. That is, consider a system
of the form
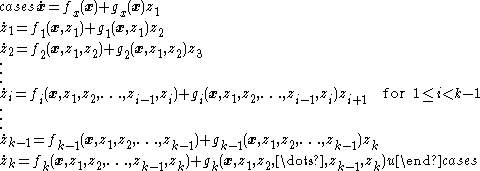
where
Also assume that the subsystem
is stabilized
to the origin
(i.e., ) by some known control
) by some known control  such that
such that 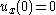 . It is also assumed that a Lyapunov function
. It is also assumed that a Lyapunov function
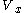 for this stable subsystem is known. That is, this
for this stable subsystem is known. That is, this 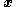 subsystem is stabilized by some other method and backstepping extends its stability to the
subsystem is stabilized by some other method and backstepping extends its stability to the 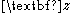 shell around it.
shell around it.
In systems of this strict-feedback form around a stable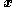 subsystem,
subsystem,
The backstepping approach determines how to stabilize the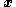 subsystem using
subsystem using 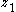 , and then proceeds with determining how to make the next state
, and then proceeds with determining how to make the next state  drive
drive  to the control required to stabilize
to the control required to stabilize 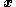 . Hence, the process "steps backward" from
. Hence, the process "steps backward" from  out of the strict-feedback form system until the ultimate control
out of the strict-feedback form system until the ultimate control  is designed.
is designed.
This process is known as backstepping because it starts with the requirements on some internal subsystem for stability and progressively steps back out of the system, maintaining stability at each step. Because
then the resulting system has an equilibrium at the origin (i.e., where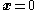 ,
, 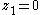 ,
,  , … ,
, … , 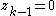 , and
, and  ) that is globally asymptotically stable.
) that is globally asymptotically stable.
s, it is convenient to discuss the approach for a smaller class of strict-feedback form systems. These systems connect a series of integrators to the input of a
system with a known feedback-stabilizing control law, and so the stabilizing approach is known as integrator backstepping. With a small modification, the integrator backstepping approach can be extended to handle all strict-feedback form systems.
where and
and  is a scalar. This system is a cascade connection of an integrator
is a scalar. This system is a cascade connection of an integrator
with the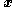 subsystem (i.e., the input
subsystem (i.e., the input  enters an integrator, and the integral
enters an integrator, and the integral
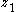 enters the
enters the  subsystem).
subsystem).
We assume that , and so if
, and so if  ,
, 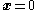 and
and  , then
, then
So the origin
 is an equilibrium (i.e., a stationary point
is an equilibrium (i.e., a stationary point
) of the system. If the system ever reaches the origin, it will remain there forever after.
the single-integrator system in Equation (1) around its equilibrium at the origin. To be less precise, we wish to design a control law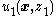 that ensures that the states
that ensures that the states 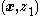 return to
return to 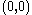 after the system is started from some arbitrary initial condition.
after the system is started from some arbitrary initial condition.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, backstepping is a technique developed circa
Circa
Circa , usually abbreviated c. or ca. , means "approximately" in the English language, usually referring to a date...
1990 by Petar V. Kokotovic
Petar V. Kokotovic
Petar V. Kokotovic is a professor in the Department of Engineering at the University of California, Santa Barbara, USA. He has made contributions in the areas of adaptive control, singular perturbation techniques, and nonlinear control....
and others for designing stabilizing
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
controls for a special class of nonlinear dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. These systems are built from subsystems that radiate out from an irreducible subsystem that can be stabilized using some other method. Because of this recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
structure, the designer can start the design process at the known-stable system and "back out" new controllers that progressively stabilize each outer subsystem. The process terminates when the final external control is reached. Hence, this process is known as backstepping.
The backstepping approach provides a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
method for stabilizing
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of a system in strict-feedback form. That is, consider a system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
of the form
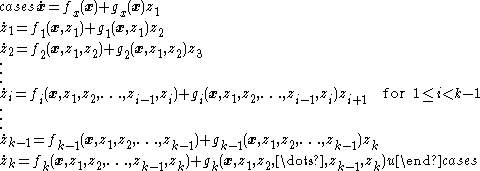
where
-
 with
with  ,
, -
 are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s, -
 is a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
is a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
input to the system, -
 vanishVanishVanish may refer to:*Vanish , a toilet bowl cleaner by S.C. Johnson or a cloth stain remover by Reckitt Benckiser*"Vanish" an episode of the TV series Criss Angel Mindfreak*Vanishing, a type of magical effect...
vanishVanishVanish may refer to:*Vanish , a toilet bowl cleaner by S.C. Johnson or a cloth stain remover by Reckitt Benckiser*"Vanish" an episode of the TV series Criss Angel Mindfreak*Vanishing, a type of magical effect...
at the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
(i.e.,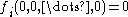 ),
), -
 are nonzero over the domain of interest (i.e.,
are nonzero over the domain of interest (i.e., 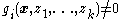 for
for  ).
).
Also assume that the subsystem

is stabilized
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
to the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
(i.e.,
 ) by some known control
) by some known control 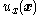 such that
such that 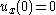 . It is also assumed that a Lyapunov function
. It is also assumed that a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
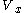 for this stable subsystem is known. That is, this
for this stable subsystem is known. That is, this 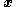 subsystem is stabilized by some other method and backstepping extends its stability to the
subsystem is stabilized by some other method and backstepping extends its stability to the 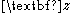 shell around it.
shell around it.In systems of this strict-feedback form around a stable
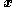 subsystem,
subsystem,
- The backstepping-designed control input
 has its most immediate stabilizing impact on state
has its most immediate stabilizing impact on state 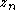 .
. - The state
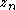 then acts like a stabilizing control on the state
then acts like a stabilizing control on the state 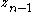 before it.
before it. - This process continues so that each state
 is stabilized by the fictitious "control"
is stabilized by the fictitious "control"  .
.
The backstepping approach determines how to stabilize the
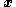 subsystem using
subsystem using 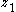 , and then proceeds with determining how to make the next state
, and then proceeds with determining how to make the next state  drive
drive  to the control required to stabilize
to the control required to stabilize 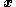 . Hence, the process "steps backward" from
. Hence, the process "steps backward" from  out of the strict-feedback form system until the ultimate control
out of the strict-feedback form system until the ultimate control  is designed.
is designed.Recursive Control Design Overview
- It is given that the smaller (i.e., lower-order) subsystem
-
- is already stabilized to the origin by some control
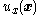 where
where  . That is, choice of
. That is, choice of  to stabilize this system must occur using some other method. It is also assumed that a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
to stabilize this system must occur using some other method. It is also assumed that a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
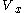 for this stable subsystem is known. Backstepping provides a way to extend the controlled stability of this subsystem to the larger system.
for this stable subsystem is known. Backstepping provides a way to extend the controlled stability of this subsystem to the larger system.
-
- A control
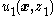 is designed so that the system
is designed so that the system
-
- is stabilized so that
 follows the desired
follows the desired 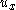 control. The control design is based on the augmented Lyapunov function candidate
control. The control design is based on the augmented Lyapunov function candidate
- The control
 can be picked to bound
can be picked to bound 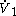 away from zero.
away from zero.
-
- A control
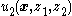 is designed so that the system
is designed so that the system
-
- is stabilized so that
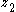 follows the desired
follows the desired  control. The control design is based on the augmented Lyapunov function candidate
control. The control design is based on the augmented Lyapunov function candidate
- The control
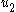 can be picked to bound
can be picked to bound 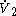 away from zero.
away from zero.
-
- This process continues until the actual
 is known, and
is known, and
- The real control
 stabilizes
stabilizes 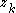 to fictitious control
to fictitious control 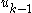 .
. - The fictitious control
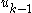 stabilizes
stabilizes 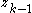 to fictitious control
to fictitious control 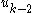 .
. - The fictitious control
 stabilizes
stabilizes  to fictitious control
to fictitious control 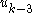 .
. - …
- The fictitious control
 stabilizes
stabilizes  to fictitious control
to fictitious control 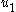 .
. - The fictitious control
 stabilizes
stabilizes 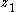 to fictitious control
to fictitious control  .
. - The fictitious control
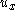 stabilizes
stabilizes 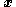 to the origin.
to the origin.
- The real control
This process is known as backstepping because it starts with the requirements on some internal subsystem for stability and progressively steps back out of the system, maintaining stability at each step. Because
-
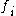 vanish at the origin for
vanish at the origin for 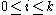 ,
, -
 are nonzero for
are nonzero for  ,
, - the given control
 has
has 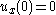 ,
,
then the resulting system has an equilibrium at the origin (i.e., where
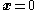 ,
, 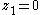 ,
,  , … ,
, … , 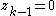 , and
, and  ) that is globally asymptotically stable.
) that is globally asymptotically stable.Integrator Backstepping
Before describing the backstepping procedure for general strict-feedback form dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, it is convenient to discuss the approach for a smaller class of strict-feedback form systems. These systems connect a series of integrators to the input of a
system with a known feedback-stabilizing control law, and so the stabilizing approach is known as integrator backstepping. With a small modification, the integrator backstepping approach can be extended to handle all strict-feedback form systems.
Single-integrator Equilibrium
Consider the dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
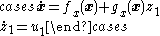 |
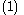 |
where
 and
and  is a scalar. This system is a cascade connection of an integrator
is a scalar. This system is a cascade connection of an integratorIntegrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
with the
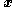 subsystem (i.e., the input
subsystem (i.e., the input  enters an integrator, and the integral
enters an integrator, and the integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
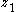 enters the
enters the  subsystem).
subsystem).We assume that
 , and so if
, and so if  ,
, 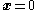 and
and  , then
, then
So the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
 is an equilibrium (i.e., a stationary point
is an equilibrium (i.e., a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
) of the system. If the system ever reaches the origin, it will remain there forever after.
Single-integrator Backstepping
In this example, backstepping is used to stabilizeLyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
the single-integrator system in Equation (1) around its equilibrium at the origin. To be less precise, we wish to design a control law
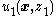 that ensures that the states
that ensures that the states 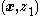 return to
return to 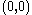 after the system is started from some arbitrary initial condition.
after the system is started from some arbitrary initial condition.- First, by assumption, the subsystem
- with
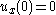 has a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
has a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
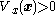 such that
such that
- where
 is a positive-definite function. That is, we assume that we have already shown that this existing simpler
is a positive-definite function. That is, we assume that we have already shown that this existing simpler 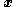 subsystem is stable (in the sense of Lyapunov)Lyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
subsystem is stable (in the sense of Lyapunov)Lyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
. Roughly speaking, this notion of stability means that:- The function
 is like a "generalized energy" of the
is like a "generalized energy" of the  subsystem. As the
subsystem. As the 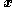 states of the system move away from the origin, the energy
states of the system move away from the origin, the energy 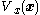 also grows.
also grows. - By showing that over time, the energy
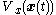 decays to zero, then the
decays to zero, then the 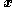 states must decay toward
states must decay toward 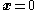 . That is, the origin
. That is, the origin 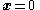 will be a stable equilibrium of the system – the
will be a stable equilibrium of the system – the 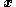 states will continuously approach the origin as time increases.
states will continuously approach the origin as time increases. - Saying that
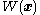 is positive definite means that
is positive definite means that  everywhere except for
everywhere except for  , and
, and  .
. - The statement that
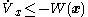 means that
means that  is bounded away from zero for all points except where
is bounded away from zero for all points except where 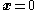 . That is, so long as the system is not at its equilibrium at the origin, its "energy" will be decreasing.
. That is, so long as the system is not at its equilibrium at the origin, its "energy" will be decreasing. - Because the energy is always decaying, then the system must be stable; its trajectories must approach the origin.
- The function
- Our task is to find a control
 that makes our cascaded
that makes our cascaded  system also stable. So we must find a new Lyapunov function candidate for this new system. That candidate will depend upon the control
system also stable. So we must find a new Lyapunov function candidate for this new system. That candidate will depend upon the control  , and by choosing the control properly, we can ensure that it is decaying everywhere as well.
, and by choosing the control properly, we can ensure that it is decaying everywhere as well.
- Next, by adding and subtracting
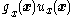 (i.e., we don't change the system in any way because we make no net effect) to the
(i.e., we don't change the system in any way because we make no net effect) to the  part of the larger
part of the larger 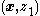 system, it becomes
system, it becomes
- which we can re-group to get
- So our cascaded supersystem encapsulates the known-stable
 subsystem plus some error perturbation generated by the integrator.
subsystem plus some error perturbation generated by the integrator.
- We now can change variables from
 to
to  by letting
by letting  . So
. So
-

- Additionally, we let
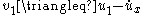 so that
so that  and
and
- We seek to stabilize this error system by feedback through the new control
 . By stabilizing the system at
. By stabilizing the system at  , the state
, the state 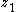 will track the desired control
will track the desired control  which will result in stabilizing the inner
which will result in stabilizing the inner 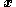 subsystem.
subsystem.
- From our existing Lyapunov function
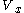 , we define the augmented Lyapunov function candidate
, we define the augmented Lyapunov function candidate
- By distributing
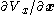 , we see that
, we see that
- To ensure that
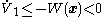 (i.e., to ensure stability of the supersystem), we pick the control law
(i.e., to ensure stability of the supersystem), we pick the control law
- with
 , and so
, and so
- After distributing the
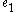 through,
through,
-

- So our candidate Lyapunov function
 is a true Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
is a true Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
, and our system is stable under this control law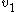 (which corresponds the control law
(which corresponds the control law  because
because 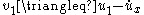 ). Using the variables from the original coordinate system, the equivalent Lyapunov function
). Using the variables from the original coordinate system, the equivalent Lyapunov function
- {| border="0", width="75%"
|-
|align="left"|
|align="right"|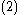
|-
|}- As discussed below, this Lyapunov function will be used again when this procedure is applied iteratively to multiple-integrator problem.
- Our choice of control
 ultimately depends on all of our original state variables. In particular, the actual feedback-stabilizing control law
ultimately depends on all of our original state variables. In particular, the actual feedback-stabilizing control law
-
- {| border="0", width="75%"
|-
|align="left"|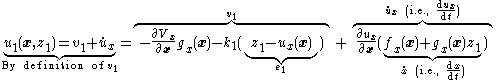
|align="right"|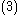
|-
|}- The states
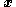 and
and 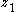 and functions
and functions 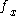 and
and  come from the system. The function
come from the system. The function  comes from our known-stable
comes from our known-stable  subsystem. The gain parameter
subsystem. The gain parameter  affects the convergence rate or our system. Under this control law, our system is stableLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
affects the convergence rate or our system. Under this control law, our system is stableLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
at the origin .
.
- Recall that
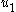 in Equation (3) drives the input of an integrator that is connected to a subsystem that is feedback-stabilized by the control law
in Equation (3) drives the input of an integrator that is connected to a subsystem that is feedback-stabilized by the control law 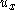 . Not surprisingly, the control
. Not surprisingly, the control  has a
has a  term that will be integrated to follow the stabilizing control law
term that will be integrated to follow the stabilizing control law  plus some offset. The other terms provide damping to remove that offset and any other perturbation effects that would be magnified by the integrator.
plus some offset. The other terms provide damping to remove that offset and any other perturbation effects that would be magnified by the integrator.
So because this system is feedback stabilized by and has Lyapunov function
and has Lyapunov function  with
with 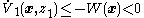 , it can be used as the upper subsystem in another single-integrator cascade system.
, it can be used as the upper subsystem in another single-integrator cascade system.
Motivating Example: Two-integrator Backstepping
Before discussing the recursive procedure for the general multiple-integrator case, it is instructive to study the recursion present in the two-integrator case. That is, consider the dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
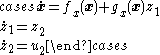
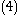
where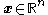 and
and  and
and 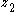 are scalars. This system is a cascade connection of the single-integrator system in Equation (1) with another integrator (i.e., the input
are scalars. This system is a cascade connection of the single-integrator system in Equation (1) with another integrator (i.e., the input 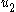 enters through an integrator, and the output of that integrator enters the system in Equation (1) by its
enters through an integrator, and the output of that integrator enters the system in Equation (1) by its  input).
input).
By letting-
 ,
, -
 ,
, -

then the two-integrator system in Equation (4) becomes the single-integrator system
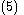
By the single-integrator procedure, the control law stabilizes the upper
stabilizes the upper  -to-
-to-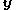 subsystem using the Lyapunov function
subsystem using the Lyapunov function 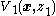 , and so Equation (5) is a new single-integrator system that is structurally equivalent to the single-integrator system in Equation (1). So a stabilizing control
, and so Equation (5) is a new single-integrator system that is structurally equivalent to the single-integrator system in Equation (1). So a stabilizing control  can be found using the same single-integrator procedure that was used to find
can be found using the same single-integrator procedure that was used to find 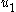 .
.
Many-integrator backstepping
In the two-integrator case, the upper single-integrator subsystem was stabilized yielding a new single-integrator system that can be similarly stabilized. This recursive procedure can be extended to handle any finite number of integrators. This claim can be formally proved with mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Here, a stabilized multiple-integrator system is built up from subsystems of already-stabilized multiple-integrator subsystems.
- First, consider the dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
-
- that has scalar input
 and output states
and output states  . Assume that
. Assume that
 so that the zero-input (i.e.,
so that the zero-input (i.e., 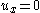 ) system is stationaryStationary pointIn mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
) system is stationaryStationary pointIn mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
at the origin . In this case, the origin is called an equilibrium of the system.
. In this case, the origin is called an equilibrium of the system.- The feedback control law
 stabilizes the system at the equilibrium at the origin.
stabilizes the system at the equilibrium at the origin. - A Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
corresponding to this system is described by .
.
- That is, if output states
 are fed back to the input
are fed back to the input 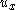 by the control law
by the control law 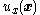 , then the output states (and the Lyapunov function) return to the origin after a single perturbation (e.g., after a nonzero initial condition or a sharp disturbance). This subsystem is stabilized by feedback control law
, then the output states (and the Lyapunov function) return to the origin after a single perturbation (e.g., after a nonzero initial condition or a sharp disturbance). This subsystem is stabilized by feedback control law  .
.
- Next, connect an integratorIntegratorAn integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
to input so that the augmented system has input
so that the augmented system has input 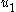 (to the integrator) and output states
(to the integrator) and output states 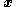 . The resulting augmented dynamical system is
. The resulting augmented dynamical system is
-
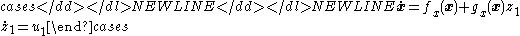
- This "cascade" system matches the form in Equation (1), and so the single-integrator backstepping procedure leads to the stabilizing control law in Equation (3). That is, if we feed back states
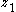 and
and 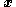 to input
to input 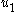 according to the control law
according to the control law
- with gain
 , then the states
, then the states 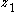 and
and 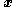 will return to
will return to 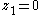 and
and 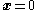 after a single perturbation. This subsystem is stabilized by feedback control law
after a single perturbation. This subsystem is stabilized by feedback control law  , and the corresponding Lyapunov function from Equation (2) is
, and the corresponding Lyapunov function from Equation (2) is
- That is, under feedback control law
 , the Lyapunov function
, the Lyapunov function 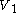 decays to zero as the states return to the origin.
decays to zero as the states return to the origin.
- Connect a new integrator to input
 so that the augmented system has input
so that the augmented system has input 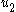 and output states
and output states  . The resulting augmented dynamical system is
. The resulting augmented dynamical system is
-

- which is equivalent to the single-integrator system
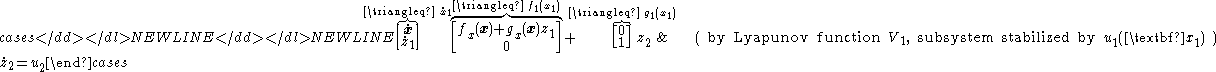
- Using these definitions of
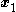 ,
, 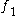 , and
, and  , this system can also be expressed as
, this system can also be expressed as

- This system matches the single-integrator structure of Equation (1), and so the single-integrator backstepping procedure can be applied again. That is, if we feed back states
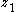 ,
, 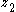 , and
, and  to input
to input  according to the control law
according to the control law
- with gain
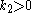 , then the states
, then the states  ,
, 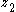 , and
, and  will return to
will return to  ,
, 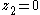 , and
, and  after a single perturbation. This subsystem is stabilized by feedback control law
after a single perturbation. This subsystem is stabilized by feedback control law  , and the corresponding Lyapunov function is
, and the corresponding Lyapunov function is
- That is, under feedback control law
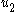 , the Lyapunov function
, the Lyapunov function  decays to zero as the states return to the origin.
decays to zero as the states return to the origin.
- Connect an integrator to input
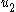 so that the augmented system has input
so that the augmented system has input 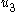 and output states
and output states  . The resulting augmented dynamical system is
. The resulting augmented dynamical system is
-

- which can be re-grouped as the single-integrator system
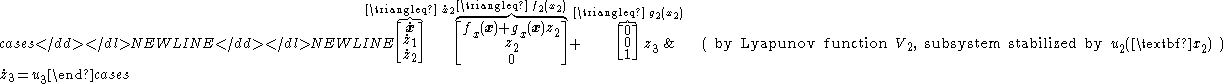
- By the definitions of
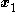 ,
, 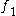 , and
, and 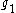 from the previous step, this system is also represented by
from the previous step, this system is also represented by

- Further, using these definitions of
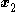 ,
, 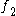 , and
, and 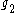 , this system can also be expressed as
, this system can also be expressed as
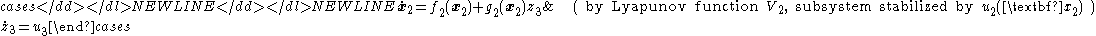
- So the re-grouped system has the single-integrator structure of Equation (1), and so the single-integrator backstepping procedure can be applied again. That is, if we feed back states
 ,
,  ,
, 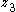 , and
, and 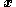 to input
to input  according to the control law
according to the control law
- with gain
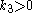 , then the states
, then the states  ,
, 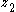 ,
, 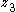 , and
, and  will return to
will return to  ,
,  ,
,  , and
, and  after a single perturbation. This subsystem is stabilized by feedback control law
after a single perturbation. This subsystem is stabilized by feedback control law 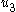 , and the corresponding Lyapunov function is
, and the corresponding Lyapunov function is
- That is, under feedback control law
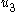 , the Lyapunov function
, the Lyapunov function 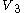 decays to zero as the states return to the origin.
decays to zero as the states return to the origin.
- This process can continue for each integrator added to the system, and hence any system of the form
-

- has the recursive structure
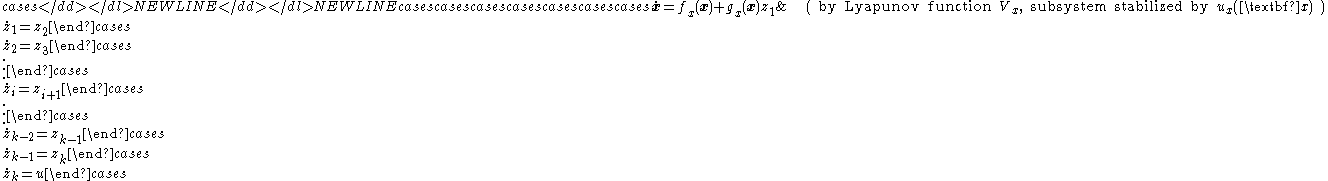
- and can be feedback stabilized by finding the feedback-stabilizing control and Lyapunov function for the single-integrator
 subsystem (i.e., with input
subsystem (i.e., with input 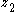 and output
and output  ) and iterating out from that inner subsystem until the ultimate feedback-stabilizing control
) and iterating out from that inner subsystem until the ultimate feedback-stabilizing control  is known. At iteration
is known. At iteration  , the equivalent system is
, the equivalent system is

- The corresponding feedback-stabilizing control law is
- with gain
 . The corresponding Lyapunov function is
. The corresponding Lyapunov function is
- By this construction, the ultimate control
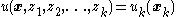 (i.e., ultimate control is found at final iteration
(i.e., ultimate control is found at final iteration 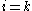 ).
).
Hence, any system in this special many-integrator strict-feedback form can be feedback stabilized using a straightforward procedure that can even be automated (e.g., as part of an adaptive controlAdaptive controlAdaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself...
algorithm).
Generic Backstepping
Systems in the special strict-feedback form have a recursive structure similar to the many-integrator system structure. Likewise, they are stabilized by stabilizing the smallest cascaded system and then backstepping to the next cascaded system and repeating the procedure. So it is critical to develop a single-step procedure; that procedure can be recursively applied to cover the many-step case. Fortunately, due to the requirements on the functions in the strict-feedback form, each single-step system can be rendered by feedback to a single-integrator system, and that single-integrator system can be stabilized using methods discussed above.
Single-step Procedure
Consider the simple strict-feedback systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

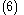
where-
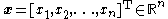 ,
, -
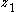 and
and 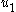 are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s, - For all
 and
and  ,
, 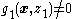 .
.
Rather than designing feedback-stabilizing control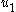 directly, introduce a new control
directly, introduce a new control  (to be designed later) and use control law
(to be designed later) and use control law
which is possible because . So the system in Equation (6) is
. So the system in Equation (6) is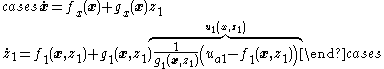
which simplifies to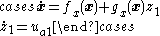
This new -to-
-to-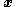 system matches the single-integrator cascade system in Equation (1). Assuming that a feedback-stabilizing control law
system matches the single-integrator cascade system in Equation (1). Assuming that a feedback-stabilizing control law 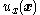 and Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
and Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
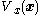 for the upper subsystem is known, the feedback-stabilizing control law from Equation (3) is
for the upper subsystem is known, the feedback-stabilizing control law from Equation (3) is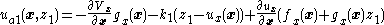
with gain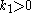 . So the final feedback-stabilizing control law is
. So the final feedback-stabilizing control law is

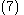
with gain . The corresponding Lyapunov function from Equation (2) is
. The corresponding Lyapunov function from Equation (2) is
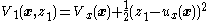
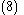
Because this strict-feedback system has a feedback-stabilizing control and a corresponding Lyapunov function, it can be cascaded as part of a larger strict-feedback system, and this procedure can be repeated to find the surrounding feedback-stabilizing control.
Many-step Procedure
As in many-integrator backstepping, the single-step procedure can be completed iteratively to stabilize an entire strict-feedback system. In each step,- The smallest "unstabilized" single-step strict-feedback system is isolated.
- Feedback is used to convert the system into a single-integrator system.
- The resulting single-integrator system is stabilized.
- The stabilized system is used as the upper system in the next step.
That is, any strict-feedback system
has the recursive structure
and can be feedback stabilized by finding the feedback-stabilizing control and Lyapunov function for the single-integrator subsystem (i.e., with input
subsystem (i.e., with input 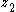 and output
and output  ) and iterating out from that inner subsystem until the ultimate feedback-stabilizing control
) and iterating out from that inner subsystem until the ultimate feedback-stabilizing control  is known. At iteration
is known. At iteration 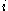 , the equivalent system is
, the equivalent system is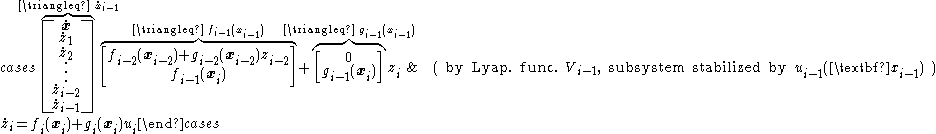
By Equation (7), the corresponding feedback-stabilizing control law is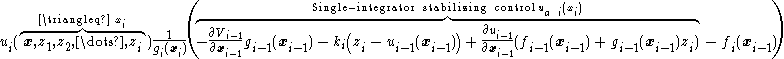
with gain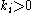 . By Equation (8), the corresponding Lyapunov function is
. By Equation (8), the corresponding Lyapunov function is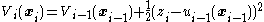
By this construction, the ultimate control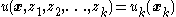 (i.e., ultimate control is found at final iteration
(i.e., ultimate control is found at final iteration 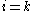 ).
).
Hence, any strict-feedback system can be feedback stabilized using a straightforward procedure that can even be automated (e.g., as part of an adaptive controlAdaptive controlAdaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself...
algorithm).
See also
- Nonlinear controlNonlinear controlNonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
- Strict-feedback form
- Robust controlRobust controlRobust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
- Adaptive controlAdaptive controlAdaptive control is the control method used by a controller which must adapt to a controlled system with parameters which vary, or are initially uncertain. For example, as an aircraft flies, its mass will slowly decrease as a result of fuel consumption; a control law is needed that adapts itself...
- The corresponding feedback-stabilizing control law is
- and can be feedback stabilized by finding the feedback-stabilizing control and Lyapunov function for the single-integrator
- has the recursive structure
- So the re-grouped system has the single-integrator structure of Equation (1), and so the single-integrator backstepping procedure can be applied again. That is, if we feed back states
- Further, using these definitions of
- By the definitions of
- which can be re-grouped as the single-integrator system
- This system matches the single-integrator structure of Equation (1), and so the single-integrator backstepping procedure can be applied again. That is, if we feed back states
- Using these definitions of
- which is equivalent to the single-integrator system
- This "cascade" system matches the form in Equation (1), and so the single-integrator backstepping procedure leads to the stabilizing control law in Equation (3). That is, if we feed back states
- So our candidate Lyapunov function
- Additionally, we let