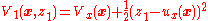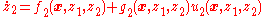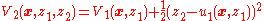Strict-feedback form
Encyclopedia
In control theory
, dynamical systems
are in strict-feedback form when they can be expressed as
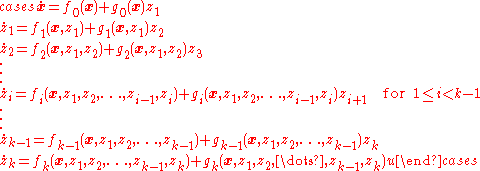
where
Here, strict feedback refers to the fact that the nonlinear functions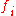 and
and 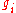 in the
in the 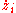 equation only depend on states
equation only depend on states  that are fed back to that subsystem. That is, the system has a kind of lower triangular
that are fed back to that subsystem. That is, the system has a kind of lower triangular
form.
Systems in strict-feedback form can be stabilized
by recursive application of backstepping
. That is,
This process is known as backstepping because it starts with the requirements on some internal subsystem for stability and progressively steps back out of the system, maintaining stability at each step. Because
then the resulting system has an equilibrium at the origin (i.e., where ,
,  ,
, 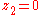 , … ,
, … , 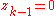 , and
, and  ) that is globally asymptotically stable.
) that is globally asymptotically stable.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, dynamical systems
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
are in strict-feedback form when they can be expressed as
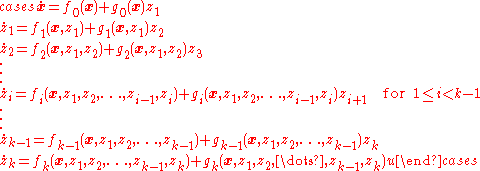
where
-
 with
with  ,
, -
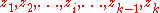 are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
are scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s, -
 is a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
is a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
input to the system, -
 vanishVanishVanish may refer to:*Vanish , a toilet bowl cleaner by S.C. Johnson or a cloth stain remover by Reckitt Benckiser*"Vanish" an episode of the TV series Criss Angel Mindfreak*Vanishing, a type of magical effect...
vanishVanishVanish may refer to:*Vanish , a toilet bowl cleaner by S.C. Johnson or a cloth stain remover by Reckitt Benckiser*"Vanish" an episode of the TV series Criss Angel Mindfreak*Vanishing, a type of magical effect...
at the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
(i.e., ),
), -
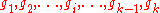 are nonzero over the domain of interest (i.e.,
are nonzero over the domain of interest (i.e.,  for
for  ).
).
Here, strict feedback refers to the fact that the nonlinear functions
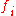 and
and 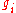 in the
in the 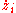 equation only depend on states
equation only depend on states  that are fed back to that subsystem. That is, the system has a kind of lower triangular
that are fed back to that subsystem. That is, the system has a kind of lower triangularTriangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
form.
Stabilization
Systems in strict-feedback form can be stabilized
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
by recursive application of backstepping
Backstepping
In control theory, backstepping is a technique developed circa 1990 by Petar V. Kokotovic and others for designing stabilizing controls for a special class of nonlinear dynamical systems. These systems are built from subsystems that radiate out from an irreducible subsystem that can be stabilized...
. That is,
- It is given that the system
-
- is already stabilized to the origin by some control
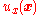 where
where 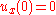 . That is, choice of
. That is, choice of 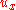 to stabilize this system must occur using some other method. It is also assumed that a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
to stabilize this system must occur using some other method. It is also assumed that a Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
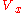 for this stable subsystem is known.
for this stable subsystem is known.
-
- A control
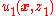 is designed so that the system
is designed so that the system
-
- is stabilized so that
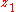 follows the desired
follows the desired 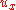 control. The control design is based on the augmented Lyapunov function candidate
control. The control design is based on the augmented Lyapunov function candidate
- The control
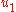 can be picked to bound
can be picked to bound 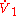 away from zero.
away from zero.
-
- A control
 is designed so that the system
is designed so that the system
-
- is stabilized so that
 follows the desired
follows the desired 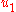 control. The control design is based on the augmented Lyapunov function candidate
control. The control design is based on the augmented Lyapunov function candidate
- The control
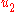 can be picked to bound
can be picked to bound  away from zero.
away from zero.
-
- This process continues until the actual
 is known, and
is known, and
- The real control
 stabilizes
stabilizes 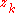 to fictitious control
to fictitious control 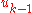 .
. - The fictitious control
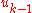 stabilizes
stabilizes 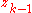 to fictitious control
to fictitious control 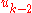 .
. - The fictitious control
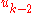 stabilizes
stabilizes 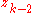 to fictitious control
to fictitious control  .
. - …
- The fictitious control
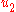 stabilizes
stabilizes  to fictitious control
to fictitious control 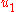 .
. - The fictitious control
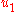 stabilizes
stabilizes 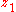 to fictitious control
to fictitious control 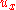 .
. - The fictitious control
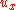 stabilizes
stabilizes  to the origin.
to the origin.
- The real control
This process is known as backstepping because it starts with the requirements on some internal subsystem for stability and progressively steps back out of the system, maintaining stability at each step. Because
-
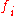 vanish at the origin for
vanish at the origin for  ,
, -
 are nonzero for
are nonzero for 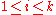 ,
, - the given control
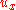 has
has  ,
,
then the resulting system has an equilibrium at the origin (i.e., where
 ,
,  ,
, 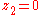 , … ,
, … , 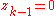 , and
, and  ) that is globally asymptotically stable.
) that is globally asymptotically stable.