
Baer ring
Encyclopedia
In abstract algebra
and functional analysis
, Baer rings, Baer *-rings, Rickart rings, Rickart *-rings, and AW* algebras are various attempts to give an algebraic analogue of von Neumann algebra
s, using axioms about annihilator
s of various sets.
Any von Neumann algebra is a Baer *-ring, and much of the theory of projections in von Neumann algebras can be extended to all Baer *-rings, For example, Baer *-rings can be divided into types I, II, and III in the same way as von Neumann algebras.
In the literature, left Rickart rings have also been termed left PP-rings. ("Principal implies projective": See definitions below.)
In operator theory, the definitions are strengthened slightly by requiring the ring R to have an involution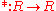 . Since this makes R isomorphic to its opposite ring
. Since this makes R isomorphic to its opposite ring
Rop, the definition of Rickart *-ring is left-right symmetric.
if the ring is a Baer *-ring.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Baer rings, Baer *-rings, Rickart rings, Rickart *-rings, and AW* algebras are various attempts to give an algebraic analogue of von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s, using axioms about annihilator
Annihilator
Annihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
s of various sets.
Any von Neumann algebra is a Baer *-ring, and much of the theory of projections in von Neumann algebras can be extended to all Baer *-rings, For example, Baer *-rings can be divided into types I, II, and III in the same way as von Neumann algebras.
In the literature, left Rickart rings have also been termed left PP-rings. ("Principal implies projective": See definitions below.)
Definitions
- An idempotent in a ring is an element e with e2 = e.
- The left annihilatorAnnihilatorAnnihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
of a set is
is 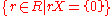
- A (left) Rickart ring is a ring satisfying any of the following conditions:
- the left annihilator of any single element of R is generated (as a left ideal) by an idempotent element.
- (For unital rings) the left annihilator of any element is a direct summand of R.
- All principal left ideals (ideals of the form Rx) are projectiveProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
R modules.- A Baer ring has the following definitions:
- The left annihilator of any subset of R is generated (as a left ideal) by an idempotent element.
- (For unital rings) The left annihilator of any subset of R is a direct summand of R. For unital rings, replacing all occurrences of 'left' with 'right' yields an equivalent definition, that is to say, the definition is left-right symmetric.
In operator theory, the definitions are strengthened slightly by requiring the ring R to have an involution
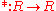 . Since this makes R isomorphic to its opposite ring
. Since this makes R isomorphic to its opposite ringOpposite ring
In algebra, the opposite of a ring is another ring with the same elements and addition operation, but with the multiplication performed in the reverse order....
Rop, the definition of Rickart *-ring is left-right symmetric.
- A projection in a *-ring is an idempotent p that is self adjoint (p*=p).
- A Rickart *-ring is a *-ring such that left annihilator of any element is generated (as a left ideal) by a projection.
- A Baer *-ring is a *-ring such that left annihilator of any subset is generated (as a left ideal) by a projection.
- An AW* algebra, introduced by , is a C* algebra that is also a Baer *-ring.
Examples
- Since the principal left ideals of a left hereditary ringHereditary ringIn mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
or left semihereditary ring are projective, it is clear that both types are left Rickart rings. This includes von Neumann regular ringVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
s, which are left and right semihereditary. If a von Neumann regular ring R is also right or left self injective, then R is Baer. - Any semisimple ring is Baer, since all left and right ideals are summands in R, including the annihilators.
- Any domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
is Baer, since all annihilators are except for the annihilator of 0, which is R, and both
except for the annihilator of 0, which is R, and both  and R are summands of R.
and R are summands of R. - The ring of bounded linear operators on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
are a Baer ring and is also a Baer *-ring with the involution * given by the adjoint. - von Neumann algebras are examples of all the different sorts of ring above.
Properties
The projections in a Rickart *-ring form a lattice, which is completeComplete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
if the ring is a Baer *-ring.

