In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, especially in the area of abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

 known as module theory, a ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 R is called hereditary if all submodules of projective module

Projective module

In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...

s over R are again projective. If this is required only for finitely generated submodules, it is called semihereditary.

For a noncommutative ring R, the terms left hereditary and left semihereditary and their right hand versions are used to distinguish the property on a single side of the ring. To be left (semi-)hereditary, all (finitely generated) submodules of projective left R-modules must be projective, and to be right (semi-)hereditary all (finitely generated) submodules of projective right submodules must be projective. It is possible for a ring to be left (semi-)hereditary but not right (semi-)hereditary, and vice versa.

Equivalent definitions

• The ring R is left (semi-)hereditary if and only if all (finitely generated) left ideals of R are projective modules.
• The ring R is left hereditary if and only if all left modules have projective resolutions of length at most 1. Hence the usual derived functor
  Derived functor
  In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
  
  s such as and 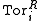are trivial for .

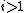Examples

• Semisimple rings are easily seen to be left and right hereditary via the equivalent definitions: all left and right ideals are summands of R, and hence are projective. By a similar token, in a von Neumann regular ring
  Von Neumann regular ring
  In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
  
   every finitely generated left and right ideal is a direct summand of R, and so von Neumann regular rings are left and right semihereditary.

• For any nonzero element x in a domain R, via the map 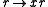. Hence in any domain, a principal right ideal is free, hence projective. This reflects the fact that domains are right Rickart rings. It follows that if R is a right Bézout domain
  Bézout domain
  In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
  
  , so that finitely generated right ideals are principal, then R has all finitely generated right ideals projective, and hence R is right semihereditary. Finally if R is assumed to be a principal right ideal domain
  Principal ideal ring
  In mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
  
  , then all right ideals are projective, and R is right hereditary.

• A commutative hereditary integral domain is called a Dedekind domain
  Dedekind domain
  In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
  
  . A commutative semi-hereditary integral domain is called a Prüfer domain
  Prüfer domain
  In mathematics, a Prüfer domain is a type of commutative ring that generalizes Dedekind domains in a non-Noetherian context. These rings possess the nice ideal and module theoretic properties of Dedekind domains, but usually only for finitely generated modules...
  
  .

• An important example of a (left) hereditary ring is the path algebra of a quiver
  Quiver (mathematics)
  In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
  
  . This is a consequence of the existence of the standard resolution (which is of length 1) for modules over a path algebra.