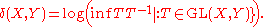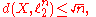Banach–Mazur compactum
Encyclopedia
In the mathematical
study of functional analysis
, the Banach–Mazur distance is a way to define a distance on the set Q(n) of n-dimensional normed spaces. If X and Y are two finite-dimensional normed spaces with the same dimension, let GL(X,Y) denote the collection of all linear isomorphisms T : X → Y. The Banach–Mazur distance between X and Y is defined by
Equipped with the metric δ, the space Q(n) is a compact metric space, called the Banach–Mazur compactum.
Many authors prefer to work with the multiplicative Banach–Mazur distance
for which d(X, Z) ≤ d(X, Y) d(Y, Z) and d(X, X) = 1.
F. John's theorem
on the maximal ellipsoid contained in a convex body gives the estimate:
where ℓn2 denotes Rn with the Euclidean norm (see the article on Lp spaces
).
From this it follows that d(X, Y) ≤ n for every couple (X, Y) in Q(n). However, for the classical spaces, this upper bound for the diameter of Q(n) is far from being approached. For example, the distance between ℓn1 and ℓn∞ is (only) of order n1/2 (up to a multiplicative constant independent from the dimension n).
A major achievement in the direction of estimating the diameter of Q(n) is due to E. Gluskin, who proved in 1981 that the (multiplicative) diameter of the Banach–Mazur compactum is bounded below by c n, for some universal c > 0.
Gluskin's method introduces a class of random symmetric polytopes P(ω) in Rn, and the normed spaces X(ω) having P(ω) as unit ball (the vector space is Rn and the norm is the gauge
of P(ω)). The proof consists in showing that the required estimate is true with large probability for two independent copies of the normed space X(ω).
Q(2) is an absolute extensor. On the other hand, Q(2) is not homeomorphic to a Hilbert cube
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the Banach–Mazur distance is a way to define a distance on the set Q(n) of n-dimensional normed spaces. If X and Y are two finite-dimensional normed spaces with the same dimension, let GL(X,Y) denote the collection of all linear isomorphisms T : X → Y. The Banach–Mazur distance between X and Y is defined by
Equipped with the metric δ, the space Q(n) is a compact metric space, called the Banach–Mazur compactum.
Many authors prefer to work with the multiplicative Banach–Mazur distance

for which d(X, Z) ≤ d(X, Y) d(Y, Z) and d(X, X) = 1.
F. John's theorem
John ellipsoid
In mathematics, the John ellipsoid E associated to a convex body K in n-dimensional Euclidean space Rn is the ellipsoid of maximal n-dimensional volume contained within K. The John ellipsoid is named after the German mathematician Fritz John...
on the maximal ellipsoid contained in a convex body gives the estimate:
where ℓn2 denotes Rn with the Euclidean norm (see the article on Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
).
From this it follows that d(X, Y) ≤ n for every couple (X, Y) in Q(n). However, for the classical spaces, this upper bound for the diameter of Q(n) is far from being approached. For example, the distance between ℓn1 and ℓn∞ is (only) of order n1/2 (up to a multiplicative constant independent from the dimension n).
A major achievement in the direction of estimating the diameter of Q(n) is due to E. Gluskin, who proved in 1981 that the (multiplicative) diameter of the Banach–Mazur compactum is bounded below by c n, for some universal c > 0.
Gluskin's method introduces a class of random symmetric polytopes P(ω) in Rn, and the normed spaces X(ω) having P(ω) as unit ball (the vector space is Rn and the norm is the gauge
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of P(ω)). The proof consists in showing that the required estimate is true with large probability for two independent copies of the normed space X(ω).
Q(2) is an absolute extensor. On the other hand, Q(2) is not homeomorphic to a Hilbert cube
Hilbert cube
In mathematics, the Hilbert cube, named after David Hilbert, is a topological space that provides an instructive example of some ideas in topology...
.