
Bapat-Beg theorem
Encyclopedia
In probability theory
, the Bapat–Beg theorem gives the joint cumulative distribution function
of order statistics of independent but not necessarily identically distributed random variable
s in terms of the cumulative distribution function
s of the random variables. A simple proof of this can be found in
Ordinarily, all elements of the sample
are obtained from the same population and thus have the same probability distribution
. The Bapat–Beg theorem describes the order statistics when each element of the sample is obtained from a possibly different population
with a different probability distribution
.
 ,
, 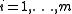 be independent real valued random variables with cumulative distribution functions
be independent real valued random variables with cumulative distribution functions 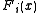 . Denote the order statistics by
. Denote the order statistics by 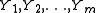 , with
, with 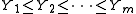 . Further let
. Further let 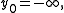
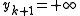 , and
, and
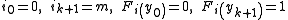
for all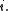 For
For 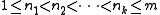 and
and 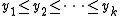 , the joint cumulative distribution function of the subset
, the joint cumulative distribution function of the subset 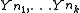 of the order statistics satisfies
of the order statistics satisfies
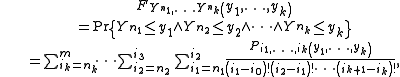
where
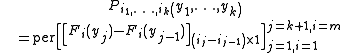
is the permanent
of a block matrix
with the subscript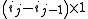 denoting the dimension of a block obtained by repeating the same entry, and the block row index
denoting the dimension of a block obtained by repeating the same entry, and the block row index 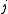 and block column index
and block column index 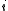 .
.
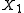 ,
, 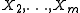 are independent and identically distributed with cumulative probability distribution function
are independent and identically distributed with cumulative probability distribution function 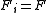 for all
for all 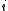 , the Bapat–Beg theorem reduces to
, the Bapat–Beg theorem reduces to
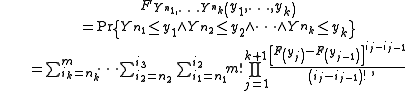
where again

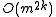 . Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.
. Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Bapat–Beg theorem gives the joint cumulative distribution function
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
of order statistics of independent but not necessarily identically distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s in terms of the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s of the random variables. A simple proof of this can be found in
Ordinarily, all elements of the sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
are obtained from the same population and thus have the same probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. The Bapat–Beg theorem describes the order statistics when each element of the sample is obtained from a possibly different population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
with a different probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
.
The theorem
Let ,
, 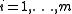 be independent real valued random variables with cumulative distribution functions
be independent real valued random variables with cumulative distribution functions 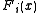 . Denote the order statistics by
. Denote the order statistics by 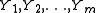 , with
, with 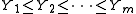 . Further let
. Further let 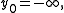
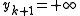 , and
, and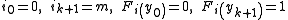
for all
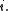 For
For 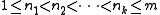 and
and 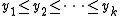 , the joint cumulative distribution function of the subset
, the joint cumulative distribution function of the subset 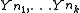 of the order statistics satisfies
of the order statistics satisfies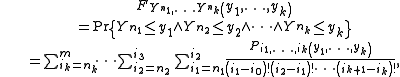
where
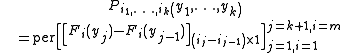
is the permanent
Permanent
The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
of a block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
with the subscript
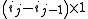 denoting the dimension of a block obtained by repeating the same entry, and the block row index
denoting the dimension of a block obtained by repeating the same entry, and the block row index 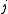 and block column index
and block column index 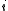 .
.The independent identically distributed case
In the case when the variables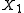 ,
, 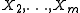 are independent and identically distributed with cumulative probability distribution function
are independent and identically distributed with cumulative probability distribution function 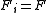 for all
for all 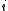 , the Bapat–Beg theorem reduces to
, the Bapat–Beg theorem reduces to 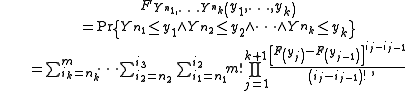
where again

Remarks
- No assumption of continuity of the cumulative distribution functions is needed.
- The theorem is formulated for the joint cumulative probability distribution function in terms of a subset of the order statistics and ordered arguments. If the inequalities
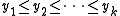 are not imposed, some of the inequalities
are not imposed, some of the inequalities 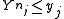 may be redundant (because always
may be redundant (because always 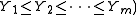 and the argument list needs to be first reduced by dropping all
and the argument list needs to be first reduced by dropping all 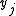 such that
such that 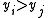 for some
for some 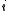 .
.
Complexity
The Bapat–Beg formula involves exponentially many permanents, and the complexity of the computation of the permanent itself is at least exponential (unless P = NP). Thus, in the general case, the formula is not practical. However, when the random variables have only two possible distributions, the complexity can be reduced to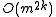 . Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.
. Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.See also
- For standard results for the distribution of order statistics for independent and identically-distributed random variables see, for example,
- permanent
- independent and identically-distributed random variables

