Baranyai's theorem
Encyclopedia
In combinatorial
mathematics, Baranyai's theorem (proved by and named after Zsolt Baranyai
) deals with the decompositions of complete hypergraph
s.
are natural numbers and r divides k, then the complete hypergraph
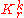decomposes into 1-factors. 
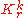is a hypergraph with k vertices, in which every subset of r vertices forms a hyperedge; a 1-factor of this hypergraph is a set of hyperedges that touches each vertex exactly once, or equivalently a partition
of the vertices into subsets of size r. Thus, the theorem states that the k vertices of the hypergraph may be partitioned into subsets of r vertices in
different ways, in such a way that each r-element subset appears in exactly one of the partitions.
with an even number of vertices has an edge coloring
whose number of colors equals its degree
, or equivalently that its edges may be partitioned into perfect matchings. It may be used to schedule round-robin tournament
s, and its solution was already known in the 19th century. The case that k = 2r is also easy.
The r = 3 case was established by R. Peltesohn in 1936. The general case was proved by Zsolt Baranyai
in 1975.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, Baranyai's theorem (proved by and named after Zsolt Baranyai
Zsolt Baranyai
Zsolt Baranyai was a Hungarian mathematician, working in combinatorics.He graduated from the Fazekas Highschool where he was a classmate of László Lovász, Miklós Laczkovich, and Lajos Pósa. Following this he learned mathematics at the Eötvös Loránd University between 1967 and 1972...
) deals with the decompositions of complete hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s.
Statement of the theorem
The statement of the result is that if are natural numbers and r divides k, then the complete hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
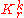decomposes into 1-factors. 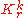is a hypergraph with k vertices, in which every subset of r vertices forms a hyperedge; a 1-factor of this hypergraph is a set of hyperedges that touches each vertex exactly once, or equivalently a partitionPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the vertices into subsets of size r. Thus, the theorem states that the k vertices of the hypergraph may be partitioned into subsets of r vertices in
different ways, in such a way that each r-element subset appears in exactly one of the partitions.History
The r = 2 case can be rephrased as stating that every complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
with an even number of vertices has an edge coloring
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
whose number of colors equals its degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
, or equivalently that its edges may be partitioned into perfect matchings. It may be used to schedule round-robin tournament
Round-robin tournament
A round-robin tournament is a competition "in which each contestant meets all other contestants in turn".-Terminology:...
s, and its solution was already known in the 19th century. The case that k = 2r is also easy.
The r = 3 case was established by R. Peltesohn in 1936. The general case was proved by Zsolt Baranyai
Zsolt Baranyai
Zsolt Baranyai was a Hungarian mathematician, working in combinatorics.He graduated from the Fazekas Highschool where he was a classmate of László Lovász, Miklós Laczkovich, and Lajos Pósa. Following this he learned mathematics at the Eötvös Loránd University between 1967 and 1972...
in 1975.