Barycentric subdivision
Encyclopedia
In geometry
, the barycentric subdivision is a standard way of dividing an arbitrary convex
polygon
into triangles, a convex polyhedron
into tetrahedra
, or, in general, a convex polytope
into simplices
with the same dimension
, by connecting the barycenter
s of their faces
in a specific way.
The name is also used in topology
for a similar operation on cell complexes. The result is topologically equivalent
to that of the geometric operation, but the parts have arbitrary shape and size.
Both operations have a number of applications in mathematics
and in geometric modeling
, especially whenever some function
or shape needs to be approximated piecewise, e.g. by a spline
.
The barycentric subdivision (henceforth BCS) of an 
-dimensional simplex
consists of (n + 1)!
simplices. Each piece, with vertices
, can be associated with a permutation
of the vertices of 
, in such a way that each vertex 
is the barycenter
of the points
.
In particular, the BCS of a single point (a 0-dimensional simplex) consists of that point itself. The BCS of a line segment (1-simplex)
consists of two smaller segments, each connecting one endpoint (0-dimensional face) of 
to the midpoint of 
itself (1-dimensional face).
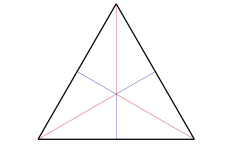
The BCS of a triangle
divides it into six triangles; each part has one vertex 
at the barycenter of 
, another one 
at the midpoint of some side, and the last one 
at one of the original vertices.
The BCS of a tetrahedron
divides it into 24 tetrahedra; each part has one vertex at the center of 
, one on some face, one along some edge, and the last one at some vertex of 
.
An important feature of BCS is the fact that the maximal diameter of an
dimensional simplex shrinks at least by the factor 
.
is to associate each part to a sequence 
of faces
of
, with increasing dimensions, such that 
is a facet of 
, for 
from 0 to 
. Then each vertex 
of the corresponding piece is the barycenter of face 
.
This alternative definition can be extended to the BCS of an arbitrary
-dimensional convex polytope into a number of 
-simplices. Thus the BCS of a pentagon
, for example, has 10 triangles: each triangle is associated to three elements 
of 
— respectively, a corner of 
, a side of 
incident to that corner, and 
itself.
Similarly the BCS of a cube
consists of 48 tetrahedra, each of them associated to a sequence
of nested elements — a vertex, an edge, a face, and the whole cube. Note that there are 8 choices for 
, 3 for 
(given 
), and 2 for 
(given 
).
theory, where it is used as a means of obtaining finer simplicial complexes (containing the original ones, i.e. with more simplices). This in turn is crucial to the simplicial approximation theorem
, which roughly states that one can approximate any continuous function between polyhedra by a (finite) simplicial map
, given a sufficient amount of subdivision of the respective simplicial complexes whom they realize. Ultimately, this approximation technique is a standard ingredient in the proof that simplicial homology groups are topological invariants.
A generalization of barycentric subdivision can also be defined for a cell complex. Informally, such object can be thought of an assemblage of one or more chunks of rubber (cells), each shaped like a convex polytope, which are glued to each other by their facets — possibly with much stretching and twisting.
The topological version of BCS replaces each cell by an assemblage of rubber simplices, likewise glued together by their facets and possibly deformed. The procedure is (1) select for each cell a deformation map
that converts it into a geometric convex polytope, preserving its incidence and topological connections; (2) perform the geometric BCS on this polytope; and, then (3) map the resulting subdivision back to the original cells.
The result of barycentric subdivision, when viewed as an abstract simplicial complex
, is an example of a flag complex. It has one vertex for every cell of the original cell complex and one maximal-dimensional cell for every flag (a collection of cells of different dimensions, all related to each other by inclusion) of the original cell complex.
, in fact). A typical application is modeling
the shape of a car
body by a spline
— a piecewise-defined polynomial
function
. The algebra of such functions becomes much simpler and easier to program if each "piece" is a "topological triangle", i.e. is attached to exactly three other pieces. However, a human user may find it more natural to design the shape by joining patches with more liberal shapes and topologies. Barycentric subdivision is a convenient way to convert that "user-friendly" model into a "computer-friendly" one.
In theory, BCS could be used for that purpose, since it has the property that the longest edge of any piece is smaller than the longest edge of the original polytope by a factor less than
. Therefore, by applying BCS sufficiently many times, the largest edge can be made as small as desired.
However, in practice BCS is not well-suited for that purpose. For one thing, each application after the first one multiplies the number of simplices by
. BCS also multiplies the degree
of each original vertex by
, and the degree of each edge by 
. Moreover, the BCS will split all simplices, even those that are already small enough. Finally, each BCS stage also makes the simplices not only smaller but "skinnier", i.e. it tends to increase their aspect ratio (the ratio between the longest and shortest edge). For all these reasons, in practice one rarely applies more than one round of BCS, and other subdivision schemes are used instead.
one defines the relative barycentric subdivision 
of 
modulo 
that consists of those simplixes with vertices 
associated to a sequence 
of proper faces of 
and barycenters 
of simplexes in 
.
Clearly,
remains a subcomplex of 
. Only the simplexes away from 
shrink.
into simplices that have one vertex at the centroid of 
, and the opposite facet on the boundary of 
. While this property holds for the true barycentric subdivision, it also holds for other subdivisions which are not the BCS.
For example, if one makes a straight cut from the barycenter of a triangle to each of its three corners, one obtains a subdivision into three triangles. Generalizing this idea, one obtains a schema for subdividing an
-dimensional simplex into 
simplices. However, this subdivision is not the BCS.
s, in a way that is compatible (with respect to the topological realization functor) with the above division of simplices.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the barycentric subdivision is a standard way of dividing an arbitrary convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
into triangles, a convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
into tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, or, in general, a convex polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
into simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
with the same dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, by connecting the barycenter
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
s of their faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
in a specific way.
The name is also used in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
for a similar operation on cell complexes. The result is topologically equivalent
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to that of the geometric operation, but the parts have arbitrary shape and size.
Both operations have a number of applications in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and in geometric modeling
Geometric modeling
Geometric modeling is a branch of applied mathematics and computational geometry that studies methods and algorithms for the mathematical description of shapes....
, especially whenever some function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
or shape needs to be approximated piecewise, e.g. by a spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
.
Barycentric subdivision of a simplex
-dimensional simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
consists of (n + 1)!Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
simplices. Each piece, with vertices
, can be associated with a permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the vertices of , in such a way that each vertex is the barycenterCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the points
.In particular, the BCS of a single point (a 0-dimensional simplex) consists of that point itself. The BCS of a line segment (1-simplex)
consists of two smaller segments, each connecting one endpoint (0-dimensional face) of to the midpoint of itself (1-dimensional face).The BCS of a triangle
divides it into six triangles; each part has one vertex at the barycenter of , another one at the midpoint of some side, and the last one at one of the original vertices.The BCS of a tetrahedron
divides it into 24 tetrahedra; each part has one vertex at the center of , one on some face, one along some edge, and the last one at some vertex of .An important feature of BCS is the fact that the maximal diameter of an
dimensional simplex shrinks at least by the factor .Barycentric subdivision of a convex polytope
Another way of defining the BCS of a simplex is to associate each part to a sequence of facesFace (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
of
, with increasing dimensions, such that is a facet of , for from 0 to . Then each vertex of the corresponding piece is the barycenter of face .This alternative definition can be extended to the BCS of an arbitrary
-dimensional convex polytope into a number of -simplices. Thus the BCS of a pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
, for example, has 10 triangles: each triangle is associated to three elements of — respectively, a corner of , a side of incident to that corner, and itself.Similarly the BCS of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
consists of 48 tetrahedra, each of them associated to a sequence
of nested elements — a vertex, an edge, a face, and the whole cube. Note that there are 8 choices for , 3 for (given ), and 2 for (given ).Barycentric subdivision in topology
Barycentric subdivision is an important tool in simplicial homologySimplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
theory, where it is used as a means of obtaining finer simplicial complexes (containing the original ones, i.e. with more simplices). This in turn is crucial to the simplicial approximation theorem
Simplicial approximation theorem
In mathematics, the simplicial approximation theorem is a foundational result for algebraic topology, guaranteeing that continuous mappings can be approximated by ones that are piecewise of the simplest kind. It applies to mappings between spaces that are built up from simplices — that is,...
, which roughly states that one can approximate any continuous function between polyhedra by a (finite) simplicial map
Simplicial map
In the mathematical discipline of simplicial homology theory, a simplicial map is a map between simplicial complexes with the property that the images of the vertices of a simplex always span a simplex. Note that this implies that vertices have vertices for images.Simplicial maps are thus...
, given a sufficient amount of subdivision of the respective simplicial complexes whom they realize. Ultimately, this approximation technique is a standard ingredient in the proof that simplicial homology groups are topological invariants.
A generalization of barycentric subdivision can also be defined for a cell complex. Informally, such object can be thought of an assemblage of one or more chunks of rubber (cells), each shaped like a convex polytope, which are glued to each other by their facets — possibly with much stretching and twisting.
The topological version of BCS replaces each cell by an assemblage of rubber simplices, likewise glued together by their facets and possibly deformed. The procedure is (1) select for each cell a deformation map
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
that converts it into a geometric convex polytope, preserving its incidence and topological connections; (2) perform the geometric BCS on this polytope; and, then (3) map the resulting subdivision back to the original cells.
The result of barycentric subdivision, when viewed as an abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
, is an example of a flag complex. It has one vertex for every cell of the original cell complex and one maximal-dimensional cell for every flag (a collection of cells of different dimensions, all related to each other by inclusion) of the original cell complex.
Applications
The barycentric subdivision is chiefly used to replace an arbitrarily complicated convex polytope or topological cell complex by an assemblage of pieces, all of them of bounded complexity (simplicesSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, in fact). A typical application is modeling
Geometric modeling
Geometric modeling is a branch of applied mathematics and computational geometry that studies methods and algorithms for the mathematical description of shapes....
the shape of a car
Automobile
An automobile, autocar, motor car or car is a wheeled motor vehicle used for transporting passengers, which also carries its own engine or motor...
body by a spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
— a piecewise-defined polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. The algebra of such functions becomes much simpler and easier to program if each "piece" is a "topological triangle", i.e. is attached to exactly three other pieces. However, a human user may find it more natural to design the shape by joining patches with more liberal shapes and topologies. Barycentric subdivision is a convenient way to convert that "user-friendly" model into a "computer-friendly" one.
Repeated barycentric subdivision
When approximating a mathematical function or a surface by a spline, the accuracy of the approximation is usually determined by the piece size — the bigger the pieces, the larger the error. Thus it is often necessary to split large pieces into smaller ones, in order to achieve a prescribed accuracy.In theory, BCS could be used for that purpose, since it has the property that the longest edge of any piece is smaller than the longest edge of the original polytope by a factor less than
. Therefore, by applying BCS sufficiently many times, the largest edge can be made as small as desired.However, in practice BCS is not well-suited for that purpose. For one thing, each application after the first one multiplies the number of simplices by
. BCS also multiplies the degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of each original vertex by
, and the degree of each edge by . Moreover, the BCS will split all simplices, even those that are already small enough. Finally, each BCS stage also makes the simplices not only smaller but "skinnier", i.e. it tends to increase their aspect ratio (the ratio between the longest and shortest edge). For all these reasons, in practice one rarely applies more than one round of BCS, and other subdivision schemes are used instead.Relative barycentric subdivision
For simplicial complexes one defines the relative barycentric subdivision of modulo that consists of those simplixes with vertices associated to a sequence of proper faces of and barycenters of simplexes in .Clearly,
remains a subcomplex of . Only the simplexes away from shrink.False barycentric subdivision
Sometimes the term "barycentric subdivision" is improperly used for any subdivision of a polytope into simplices that have one vertex at the centroid of , and the opposite facet on the boundary of . While this property holds for the true barycentric subdivision, it also holds for other subdivisions which are not the BCS.For example, if one makes a straight cut from the barycenter of a triangle to each of its three corners, one obtains a subdivision into three triangles. Generalizing this idea, one obtains a schema for subdividing an
-dimensional simplex into simplices. However, this subdivision is not the BCS.Simplicial sets
The barycentric division can also be defined for simplicial setSimplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s, in a way that is compatible (with respect to the topological realization functor) with the above division of simplices.
See also
- Apollonian networkApollonian networkIn combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable...
- Cell complex
- Finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
- Mesh generationMesh generationMesh generation is the practice of generating a polygonal or polyhedral mesh that approximates a geometric domain. The term "grid generation" is often used interchangeably. Typical uses are for rendering to a computer screen or for physical simulation such as finite element analysis or...
- PolytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
- splineSpline (mathematics)In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...