Simplicial homology
Encyclopedia
In mathematics
, in the area of algebraic topology
, simplicial homology is a theory with a finitary
definition, and is probably the most tangible variant of homology theory
.
Simplicial homology concerns topological spaces whose building blocks are n-simplex
es, the n-dimensional analogs of triangles. By definition, such a space is homeomorphic to a simplicial complex
(more precisely, the geometric realization of an abstract simplicial complex
). Such a homeomorphism is referred to as a triangulation of the given space. Replacing n-simplexes by their continuous images in a given topological space gives singular homology
. The simplicial homology of a simplicial complex is naturally isomorphic to the singular homology
of its geometric realization. This implies, in particular, that the simplicial homology of a space does not depend on the triangulation chosen for the space.
It has been shown that all manifold
s up to 3 dimensions allow for a triangulation. This, together with the fact that it is now possible to resolve the simplicial homology of a simplicial complex automatically and efficiently, make this theory feasible for application to real life situations, such as image analysis
, medical imaging
, and data analysis
in general.
is a formal sum of k-simplices
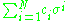, where 
is the i-th k-simplex.
The group of k-chains on S, the free abelian group
defined on the set of k-simplices in S, is denoted Ck.
Consider a basis element of Ck, a k-simplex,
The boundary operator
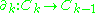
is a homomorphism defined by:
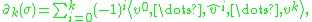
where the simplex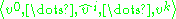
is the ith face of σ obtained by deleting its ith vertex.
In Ck, elements of the subgroup
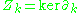
are referred to as cycles, and the subgroup
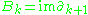
is said to consist of boundaries.
Direct computation shows that Bk lies in Zk, that is, Bk ⊆ Zk. The boundary of a boundary must be zero. In other words,
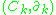
form a simplicial chain complex
.
The kth homology group Hk of S is defined to be the quotient
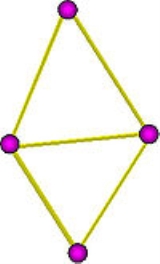
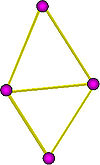
A homology group Hk is not trivial if the complex at hand contains k-cycles which are not boundaries. This indicates that there are k-dimensional holes in the complex. For example consider the complex obtained by glueing two triangles (with no interior) along one edge, shown in the image. This is a triangulation of the figure eight. The edges of each triangle form a cycle. These two cycles are by construction not boundaries (there are no 2-chains). Therefore the figure has two "1-holes".
Holes can be of different dimensions. The rank
of the homology groups, the numbers
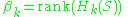
are referred to as the Betti numbers of the space S, and gives a measure of the number of k-dimensional holes in S.
In order to compute the homology groups of the triangle, one should compute the different groups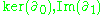 
etc. Here, by the definition of the boundary operator, we have 
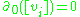, therefore the kernel is:
that is every 0-chain is in the kernel. Next, given a 1-chain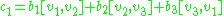
there exists: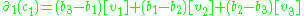
That is,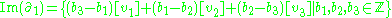
,
which means that a 0-chain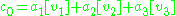
is in the image of 
if and only if
.
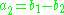
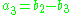This implies that we have only two degrees of freedom for choosing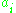
, or in other words:
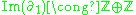
Now we can use the definition: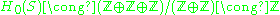
As for the other homology groups, computations are easier.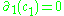
if and only if 
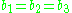, therefore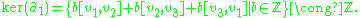
Now, since there are no 2-chains, the kernel and image of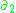
are trivial, that is 
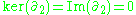. This yields:
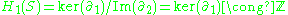
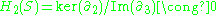
, meaning one replaces the data with a simplicial complex approximation. Computation of persistent homology (Edelsbrunner et al.2002 Robins, 1999) involves analysis of homology at different resolutions, registering homology classes (holes) that persist as the resolution is changed. Such features can be used to detect structures of molecules, tumors in X-rays, and cluster structures in complex data. A MATLAB
toolbox for computing persistent homology, Plex (Vin de Silva, Gunnar Carlsson), is available at this site.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, simplicial homology is a theory with a finitary
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
definition, and is probably the most tangible variant of homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
.
Simplicial homology concerns topological spaces whose building blocks are n-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
es, the n-dimensional analogs of triangles. By definition, such a space is homeomorphic to a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
(more precisely, the geometric realization of an abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
). Such a homeomorphism is referred to as a triangulation of the given space. Replacing n-simplexes by their continuous images in a given topological space gives singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. The simplicial homology of a simplicial complex is naturally isomorphic to the singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of its geometric realization. This implies, in particular, that the simplicial homology of a space does not depend on the triangulation chosen for the space.
It has been shown that all manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s up to 3 dimensions allow for a triangulation. This, together with the fact that it is now possible to resolve the simplicial homology of a simplicial complex automatically and efficiently, make this theory feasible for application to real life situations, such as image analysis
Image analysis
Image analysis is the extraction of meaningful information from images; mainly from digital images by means of digital image processing techniques...
, medical imaging
Medical imaging
Medical imaging is the technique and process used to create images of the human body for clinical purposes or medical science...
, and data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
in general.
Definition
Let S be a simplicial complex. A simplicial k-chainChain (algebraic topology)
In algebraic topology, a simplicial k-chainis a formal linear combination of k-simplices.-Integration on chains:Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients typically integers.The set of all k-chains forms a group...
is a formal sum of k-simplices
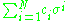, where is the i-th k-simplex.The group of k-chains on S, the free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
defined on the set of k-simplices in S, is denoted Ck.
Consider a basis element of Ck, a k-simplex,
The boundary operator
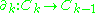
is a homomorphism defined by:
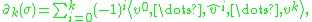
where the simplex
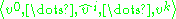
is the ith face of σ obtained by deleting its ith vertex.
In Ck, elements of the subgroup
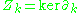
are referred to as cycles, and the subgroup
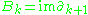
is said to consist of boundaries.
Direct computation shows that Bk lies in Zk, that is, Bk ⊆ Zk. The boundary of a boundary must be zero. In other words,
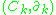
form a simplicial chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
.
A homology group Hk is not trivial if the complex at hand contains k-cycles which are not boundaries. This indicates that there are k-dimensional holes in the complex. For example consider the complex obtained by glueing two triangles (with no interior) along one edge, shown in the image. This is a triangulation of the figure eight. The edges of each triangle form a cycle. These two cycles are by construction not boundaries (there are no 2-chains). Therefore the figure has two "1-holes".
Holes can be of different dimensions. The rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of the homology groups, the numbers
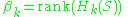
are referred to as the Betti numbers of the space S, and gives a measure of the number of k-dimensional holes in S.
Example
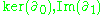etc. Here, by the definition of the boundary operator, we have 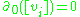, therefore the kernel is:that is every 0-chain is in the kernel. Next, given a 1-chain
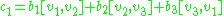there exists: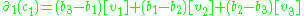That is,
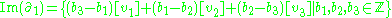,which means that a 0-chain
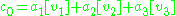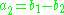
is in the image of if and only if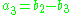.This implies that we have only two degrees of freedom for choosing
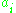, or in other words: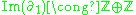Now we can use the definition:
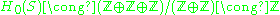
As for the other homology groups, computations are easier.
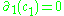if and only if 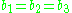, therefore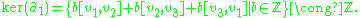Now, since there are no 2-chains, the kernel and image of
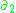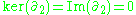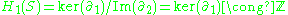
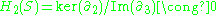
are trivial, that is . This yields:Applications
A standard scenario in many computer applications is a collection of points (measurements, dark pixels in a bit map, etc.) in which one wishes to find a topological feature. Homology can serve as a qualitative tool to search for such a feature, since it is readily computable from combinatorial data such as a simplicial complex. However, the data points have to first be triangulatedTriangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
, meaning one replaces the data with a simplicial complex approximation. Computation of persistent homology (Edelsbrunner et al.2002 Robins, 1999) involves analysis of homology at different resolutions, registering homology classes (holes) that persist as the resolution is changed. Such features can be used to detect structures of molecules, tumors in X-rays, and cluster structures in complex data. A MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
toolbox for computing persistent homology, Plex (Vin de Silva, Gunnar Carlsson), is available at this site.