
Bergman space
Encyclopedia
In complex analysis
, a branch of mathematics
, a Bergman space, named after Stefan Bergman
, is a function space
of holomorphic function
s in a domain D of the complex plane
that are sufficiently well-behaved at the boundary that they are absolutely integrable. Specifically,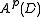 is the space of holomorphic functions in D such that the p-norm
is the space of holomorphic functions in D such that the p-norm
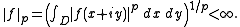
Thus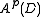 is the subspace of homolorphic functions that are in the space Lp(D)
is the subspace of homolorphic functions that are in the space Lp(D)
. The Bergman spaces are Banach space
s, which is a consequence of the estimate, valid on compact
subsets K of D:
Thus convergence of a sequence of holomorphic functions in Lp(D) implies also compact convergence
, and so the limit function is also holomorphic.
If p = 2, then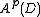 is a reproducing kernel Hilbert space
is a reproducing kernel Hilbert space
, whose kernel is given by the Bergman kernel
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Bergman space, named after Stefan Bergman
Stefan Bergman
Stefan Bergman was a Polish-born American mathematician whose primary work was in complex analysis. He is best known for the kernel function he discovered while at Berlin University in 1922. This function is known today as the Bergman kernel...
, is a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s in a domain D of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
that are sufficiently well-behaved at the boundary that they are absolutely integrable. Specifically,
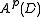 is the space of holomorphic functions in D such that the p-norm
is the space of holomorphic functions in D such that the p-normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
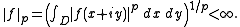
Thus
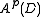 is the subspace of homolorphic functions that are in the space Lp(D)
is the subspace of homolorphic functions that are in the space Lp(D)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. The Bergman spaces are Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, which is a consequence of the estimate, valid on compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subsets K of D:
Thus convergence of a sequence of holomorphic functions in Lp(D) implies also compact convergence
Compact convergence
In mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
, and so the limit function is also holomorphic.
If p = 2, then
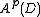 is a reproducing kernel Hilbert space
is a reproducing kernel Hilbert spaceReproducing kernel Hilbert space
In functional analysis , a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels...
, whose kernel is given by the Bergman kernel
Bergman kernel
In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cn....
.

