Bernoulli scheme
Encyclopedia
In mathematics
, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process
to more than two possible outcomes. Bernoulli schemes are important in the study of dynamical system
s, as most such systems (such as Axiom A systems) exhibit a repellor that is the product of the Cantor set
and a smooth manifold, and the dynamics on the Cantor set are isomorphic to that of the Bernoulli shift. This is essentially the Markov partition
. The term shift is in reference to the shift operator
, which may be used to study Bernoulli schemes. The Ornstein isomorphism theorem shows that Bernoulli shifts are isomorphic when their entropy is equal. Finite stationary stochastic processes are isomorphic to the Bernoulli shift; in this sense, Bernoulli shifts are universal
.
where each independent
random variable
may take on one of N distinct possible values, with the outcome i occurring with probability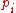
, with i = 1, ..., N, and
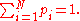
The sample space is usually denoted as
as a short-hand for
The associated measure
is
The σ-algebra
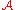on X is the product sigma algebra; that is, it is the (infinite) product of the σ-algebras of the finite set {1, ..., N}. Thus, the triplet
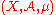
is a measure space. The Bernoulli scheme, as any stochastic process, may be viewed as a dynamical system
by endowing it with the shift operator
T where
Since the outcomes are independent, the shift preserves the measure, and thus T is a measure-preserving transformation. The quadruplet
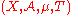
is a measure-preserving dynamical system
, and is called a Bernoulli scheme or a Bernoulli shift. It is often denoted by
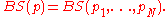
The N = 2 Bernoulli scheme is called a Bernoulli process
. The Bernoulli shift can be understood as a special case of the Markov shift, where all entries in the adjacency matrix
are one, the corresponding graph thus being a clique
.
s, are Bernoulli schemes; this is essentially the content of the Ornstein isomorphism theorem.
Ya. Sinai demonstrated that the Kolmogorov entropy of a Bernoulli scheme is given by
The isomorphism theorem for Bernoulli schemes, sometimes called the Ornstein isomorphism theorem, proven by Donald Ornstein in 1968, states that two Bernoulli schemes with the same entropy are isomorphic. Here isomorphic means that if X and Y are two sample spaces, then there exists a function between these two that is measurable and invertible, that commutes with the measures, and that commutes with the shift operators for almost all
sequences in X and Y. A simplified proof of the isomorphism theorem was given by Michael S. Keane and M. Smorodinsky in 1979.
When N is a prime number
, sequences in the sample space may be represented by p-adic number
s. If the probabilities are uniform, that is, each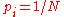
, then the distribution of sequences corresponds to a uniform measure on the space of numbers. As a result, the results from p-adic analysis
may be applied.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process
Bernoulli process
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
to more than two possible outcomes. Bernoulli schemes are important in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, as most such systems (such as Axiom A systems) exhibit a repellor that is the product of the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
and a smooth manifold, and the dynamics on the Cantor set are isomorphic to that of the Bernoulli shift. This is essentially the Markov partition
Markov partition
A Markov partition is a tool used in dynamical systems theory, allowing the methods of symbolic dynamics to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process, with the long-term dynamical characteristics...
. The term shift is in reference to the shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
, which may be used to study Bernoulli schemes. The Ornstein isomorphism theorem shows that Bernoulli shifts are isomorphic when their entropy is equal. Finite stationary stochastic processes are isomorphic to the Bernoulli shift; in this sense, Bernoulli shifts are universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
Definition
A Bernoulli scheme is a discrete-time stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
where each independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
may take on one of N distinct possible values, with the outcome i occurring with probability
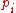, with i = 1, ..., N, and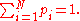The sample space is usually denoted as
as a short-hand for
The associated measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
is
The σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
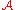on X is the product sigma algebra; that is, it is the (infinite) product of the σ-algebras of the finite set {1, ..., N}. Thus, the triplet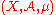is a measure space. The Bernoulli scheme, as any stochastic process, may be viewed as a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
by endowing it with the shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
T where
Since the outcomes are independent, the shift preserves the measure, and thus T is a measure-preserving transformation. The quadruplet
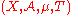
is a measure-preserving dynamical system
Measure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
, and is called a Bernoulli scheme or a Bernoulli shift. It is often denoted by
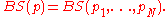
The N = 2 Bernoulli scheme is called a Bernoulli process
Bernoulli process
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
. The Bernoulli shift can be understood as a special case of the Markov shift, where all entries in the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
are one, the corresponding graph thus being a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
.
Properties
The Bernoulli scheme is a stationary stochastic process; conversely, all finite stationary stochastic processes, including subshifts of finite type and finite Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s, are Bernoulli schemes; this is essentially the content of the Ornstein isomorphism theorem.
Ya. Sinai demonstrated that the Kolmogorov entropy of a Bernoulli scheme is given by
The isomorphism theorem for Bernoulli schemes, sometimes called the Ornstein isomorphism theorem, proven by Donald Ornstein in 1968, states that two Bernoulli schemes with the same entropy are isomorphic. Here isomorphic means that if X and Y are two sample spaces, then there exists a function between these two that is measurable and invertible, that commutes with the measures, and that commutes with the shift operators for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
sequences in X and Y. A simplified proof of the isomorphism theorem was given by Michael S. Keane and M. Smorodinsky in 1979.
When N is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, sequences in the sample space may be represented by p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s. If the probabilities are uniform, that is, each
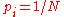, then the distribution of sequences corresponds to a uniform measure on the space of numbers. As a result, the results from p-adic analysisP-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
may be applied.