
Bertrand–Diquet–Puiseux theorem
Encyclopedia
In the mathematical
study of the differential geometry of surfaces
, the Bertrand–Diquet–Puiseux theorem
expresses the Gaussian curvature
of a surface in terms of the circumference
of a geodesic
circle, or the area of a geodesic disc. The theorem is named for Joseph Bertrand, Victor Puiseux
, and C.F. Diquet.
Let p be a point on a smooth surface M. The geodesic circle of radius r centered at p is the set of all points whose geodesic distance from p is equal to r. Let C(r) denote the circumference of this circle, and A(r) denote the area of the disc contained within the circle. The Bertrand–Diquet–Puiseux theorem asserts that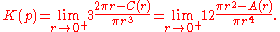
The theorem is closely related to the Gauss–Bonnet theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of the differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
, the Bertrand–Diquet–Puiseux theorem
expresses the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of a surface in terms of the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
circle, or the area of a geodesic disc. The theorem is named for Joseph Bertrand, Victor Puiseux
Victor Puiseux
Victor Alexandre Puiseux was a French mathematician and astronomer. Puiseux series are named after him, as is in part the Bertrand–Diquet–Puiseux theorem.-Life:...
, and C.F. Diquet.
Let p be a point on a smooth surface M. The geodesic circle of radius r centered at p is the set of all points whose geodesic distance from p is equal to r. Let C(r) denote the circumference of this circle, and A(r) denote the area of the disc contained within the circle. The Bertrand–Diquet–Puiseux theorem asserts that
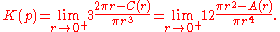
The theorem is closely related to the Gauss–Bonnet theorem
Gauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
.

