Besicovitch covering theorem
Encyclopedia
In mathematical analysis
, a Besicovitch cover, named after Abram Samoilovitch Besicovitch
, is an open cover of a subset E of the Euclidean space
RN by balls
such that each point of E is the center of some ball in the cover.
The Besicovitch covering theorem asserts that there exists a constant cN depending only on the dimension N with the following property:
Let G denote the subcollection of F consisting of all balls from the cN disjoint families A1,...,AcN.
The less precise following statement is clearly true: every point x ∈ RN belongs to at most cN different balls from the subcollection G, and G remains a cover for E (every point y ∈ E belongs to at least one ball from the subcollection G). This property gives actually an equivalent form for the theorem (except for the value of the constant).
In other words, the function SG equal to the sum of the indicator functions of the balls in G is larger than 1E and bounded on RN by the constant bN,
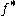by setting for every x (using the convention 
)
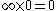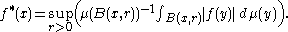
This maximal function is upper semicontinuous
, hence measurable
. The following maximal inequality is satisfied for every λ > 0 :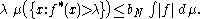
Proof.
The set Eλ of the points x such that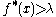
clearly admits a Besicovitch cover Fλ by balls B such that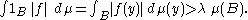
For every bounded Borel subset E´ of Eλ, one can find a subcollection G extracted from Fλ that covers E´ and such that SG ≤ bN, hence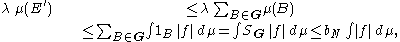
which implies the inequality above.
When dealing with the Lebesgue measure
on RN, it is more customary to use the easier (and older) Vitali covering lemma
in order to derive the previous maximal inequality (with a different constant).
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a Besicovitch cover, named after Abram Samoilovitch Besicovitch
Abram Samoilovitch Besicovitch
Abram Samoilovitch Besicovitch was a Russian mathematician, who worked mainly in England. He was born in Berdyansk on the Sea of Azov to a Karaite family.-Life and career:...
, is an open cover of a subset E of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
RN by balls
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
such that each point of E is the center of some ball in the cover.
The Besicovitch covering theorem asserts that there exists a constant cN depending only on the dimension N with the following property:
- Given any Besicovitch cover F of a bounded set E, there are cN subcollections of balls A1 = {Bn1}, …, AcN = {BncN} contained in F such that each collection Ai consists of disjoint balls, and
Let G denote the subcollection of F consisting of all balls from the cN disjoint families A1,...,AcN.
The less precise following statement is clearly true: every point x ∈ RN belongs to at most cN different balls from the subcollection G, and G remains a cover for E (every point y ∈ E belongs to at least one ball from the subcollection G). This property gives actually an equivalent form for the theorem (except for the value of the constant).
- There exists a constant bN depending only on the dimension N with the following property: Given any Besicovitch cover F of a bounded set E, there is a subcollection G of F such that G is a cover of the set E and every point x ∈ RN belongs to at most bN different balls from the subcover G.
In other words, the function SG equal to the sum of the indicator functions of the balls in G is larger than 1E and bounded on RN by the constant bN,
Application to maximal functions and maximal inequalities
Let μ be a Borel non-negative measure on RN, finite on compact subsets and let f be a μ-integrable function. Define the maximal functionMaximal function
Maximal functions appear in many forms in harmonic analysis . One of the most important of these is the Hardy–Littlewood maximal function. They play an important role in understanding, for example, the differentiability properties of functions, singular integrals and partial differential equations...
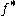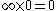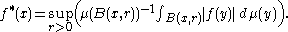
by setting for every x (using the convention )This maximal function is upper semicontinuous
Semi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
, hence measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
. The following maximal inequality is satisfied for every λ > 0 :
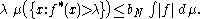
Proof.
The set Eλ of the points x such that
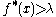clearly admits a Besicovitch cover Fλ by balls B such that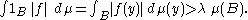For every bounded Borel subset E´ of Eλ, one can find a subcollection G extracted from Fλ that covers E´ and such that SG ≤ bN, hence
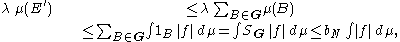
which implies the inequality above.
When dealing with the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on RN, it is more customary to use the easier (and older) Vitali covering lemma
Vitali covering lemma
In mathematics, the Vitali covering lemma is a combinatorial and geometric result commonly used in measure theory of Euclidean spaces. This lemma is an intermediate step, of independent interest, in the proof of the Vitali covering theorem. The covering theorem is credited to the Italian...
in order to derive the previous maximal inequality (with a different constant).