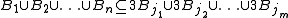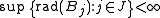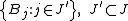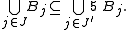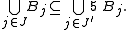Vitali covering lemma
Encyclopedia
In mathematics
, the Vitali covering lemma is a combinatorial and geometric result commonly used in measure theory of Euclidean space
s. This lemma is an intermediate step, of independent interest, in the proof of the Vitali covering theorem. The covering theorem is credited to the Italian
mathematician Giuseppe Vitali
. The theorem states that it is possible to cover, up to a Lebesgue-negligible set
, a given subset E of Rd by a disjoint family extracted from a Vitali covering of E.
Comments.
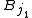be the ball of largest radius. Inductively, assume that 
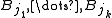have been chosen. If there is some ball in 
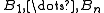that is disjoint from 
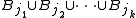, let 
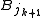be such ball with maximal radius (breaking ties arbitrarily), otherwise, we set m := k and terminate the inductive definition.
Now set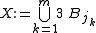
. It remains to show that 
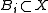for every 
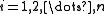. This is clear if 
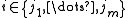. Otherwise, there necessarily is some 
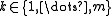such that Bi intersects 
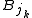and the radius of 
is at least as large as that of Bi. The triangle inequality
then easily implies that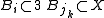
, as needed. This completes the proof of the finite version.
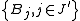, the property of G, stated below, readily proves that
Precised form of the covering lemma. Let F be a collection of (nondegenerate) balls in a metric space, with bounded radii. There exists a disjoint subcollection G of F with the following property:
(Degenerate balls only contain the center; they are excluded from this discussion.)
Let R be the supremum of the radii of balls in F. Consider the partition of F into subcollections Fn, n ≥ 0, consisting of balls B whose radius is in (2−n−1R, 2−nR]. A sequence Gn, with Gn ⊂ Fn, is defined inductively as follows. First, set H0 = F0 and let G0 be a maximal disjoint subcollection of H0. Assuming that G0,...,Gn have been selected, let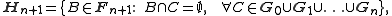
and let Gn+1 be a maximal disjoint subcollection of Hn+1. The subcollection
of F satisfies the requirements: G is a disjoint collection, and every ball B ∈ F intersects a ball C ∈ G such that B ⊂ 5 C.
Indeed, let n be such that B belongs to Fn. Either B does not belong to Hn, which implies n > 0 and means that B intersects a ball from the union of G0,...,Gn−1, or B ∈ Hn and by maximality of Gn, B intersects a ball in Gn. In any case, B intersects a ball C that belongs to the union of G0,...,Gn. Such a ball C has radius > 2−n−1R. Since the radius of B is ≤ 2−nR, it is less than twice that of C and the conclusion B ⊂ 5 C follows from the triangle inequality as in the finite version.
— Proof based on —
,
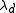, of a set E ⊂ Rd, which we know is contained in the union of a certain collection of balls 
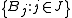, each of which has a measure we can more easily compute, or has a special property one would like to exploit. Hence, if we compute the measure of this union, we will have an upper bound on the measure of E. However, it is difficult to compute the measure of the union of all these balls if they overlap. By the Vitali lemma, we may choose a subcollection 
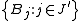which is disjoint and such that 
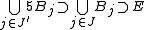. Therefore,
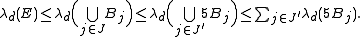
Now, since increasing the radius of a d-dimensional ball by a factor of five increases its volume by a factor of 5d, we know that
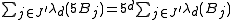
and thus
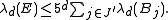
for E is a collection of sets such that, for every x ∈ E and δ > 0, there is a set U in the collection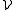 
such that x ∈ U and the diameter
of U is non-zero and less than δ.
In the classical setting of Vitali, the negligible set is a Lebesgue negligible set, but measures other than the Lebesgue measure, and spaces other than Rd have also been considered, see below.
The following observation is useful: if
is a Vitali covering for E and if E is contained in an open set Ω ⊆ Rd, then the subcollection of sets U in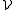 
that are contained in Ω is also a Vitali covering for E.
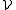of measurable subsets of Rd is a regular family (in the sense of Lebesgue
) if there exists a constant C such that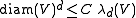
for every set V in the collection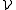
.
The family of cubes is an example of regular family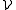
, as is the family 
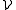(m) of rectangles in R2 such that the ratio of sides stays between m−1 and m, for some fixed m ≥ 1. If an arbitrary norm is given on Rd, the family of balls for the metric associated to the norm is another example. To the contrary, the family of all rectangles in R2 is not regular.
Theorem. Let E ⊆ Rd be a measurable set with finite Lebesgue measure, and let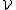
be a regular family of closed subsets of Rd that is a Vitali covering for E. Then there exists a finite or countably infinite disjoint subcollection 
such that
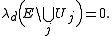
The original result of is a special case of this theorem, in which d = 1 and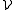
is a collection of intervals that is a Vitali covering for a measurable subset E of the real line having finite measure.
The theorem above remains true without assuming that E has finite measure. This is obtained by applying the covering result in the finite measure case, for every integer n ≥ 0, to the portion of E contained in the open annulus Ωn of points x such that n < |x| < n+1, see .
A somewhat related covering theorem is the Besicovitch covering theorem
. To each point a of a subset A ⊆ Rd, a Euclidean ball B(a, ra) with center a and positive radius ra is assigned. Then, as in the Vitali theorem, a subcollection of these balls is selected in order to cover A in a specific way. The main differences with the Vitali covering theorem are that on one hand, the disjointness requirement of Vitali is relaxed to the fact that the number Nx of the selected balls containing an arbitrary point x ∈ Rd is bounded by a constant Bd depending only upon the dimension d; on the other hand, the selected balls do cover the set A of all the given centers (for Vitali, a negligible error was allowed).
instead of Lebesgue measure. The theorem below applies in that case.
Theorem. Let Hs denote s-dimensional Hausdorff measure, let E ⊆ Rd be an Hs-measurable set and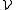
a Vitali class
of closed sets for E. Then there exists a (finite or countably infinite) disjoint subcollection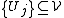
such that either
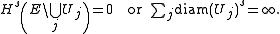
Furthermore, if E has finite s-dimensional Hausdorff measure, then for any ε > 0, we may choose this subcollection {Uj} such that
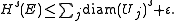
This theorem implies the result of Lebesgue given above. Indeed, when s = d, the Hausdorff measure Hs on Rd coincides with a multiple of the d-dimensional Lebesgue measure. If a disjoint collection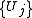
is regular and contained in a measurable region B with finite Lebesgue measure, then
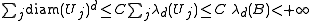
which excludes the second possibility in the first assertion of the previous theorem. It follows that E is covered, up to a Lebesgue-negligible set, by the selected disjoint subcollection.
Without loss of generality, one can assume that all balls in F are nondegenerate and have radius ≤ 1. By the precised form of the covering lemma, there exists a disjoint subcollection G of F such that every ball B ∈ F intersects a ball C ∈ G for which B ⊂ 5 C. Let r > 0 be given, and let Z denote the set of points z ∈ E that are not contained in any ball from G and belong to the open ball B(r) of radius r, centered at 0. It is enough to show that Z is Lebesgue-negligible, for every given r.
Let G denote the subcollection of those balls in G that meet B(r). Consider the partition of G into sets Gn, n ≥ 0, consisting of balls that have radius in (2−n−1, 2−n]. Any ball B in F that meets B(r) is contained in B(r+2). It follows from the disjointness property of G that
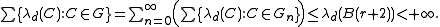
This implies that Gn is a finite set for every n. Given
ε > 0, we may select N such that
Let z ∈ Z be fixed. By definition of Z, this point z does not belong to the closed set K equal to the (finite) union of balls in Gk, k ≤ N. By the Vitali cover property, one can find a ball B ∈ F containing z, contained in B(r) and disjoint from K. By the property of G, the ball B meets C and is included in 5 C for some ball C ∈ G. One sees that C ∈ G because C intersects B(r), but C does not belong to any family Gk, k ≤ N, since B meets C but is disjoint from K. This proves that every point z ∈ Z is contained in the union of 5 C, when C varies in Gn, n > N, hence
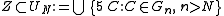
and
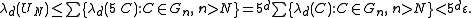
Since ε > 0 is arbitrary, this shows that Z is negligible.
Proof based on , with some notation from .
in 1979: there exists a Gaussian measure
γ on an (infinite-dimensional) separable Hilbert space
H so that the Vitali covering theorem fails for (H, Borel(H), γ). This result was strengthened in 2003 by Jaroslav Tišer: the Vitali covering theorem in fact fails for every infinite-dimensional Gaussian measure on any (infinite-dimensional) separable Hilbert space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Vitali covering lemma is a combinatorial and geometric result commonly used in measure theory of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s. This lemma is an intermediate step, of independent interest, in the proof of the Vitali covering theorem. The covering theorem is credited to the Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician Giuseppe Vitali
Giuseppe Vitali
Giuseppe Vitali was an Italian mathematician who worked in several branches of mathematical analysis.- Mathematical contributions :...
. The theorem states that it is possible to cover, up to a Lebesgue-negligible set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, a given subset E of Rd by a disjoint family extracted from a Vitali covering of E.
Statement of the lemma
- Finite version: Let
be any finite collection of ballsBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
contained in d-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd (or, more generally, in an arbitrary metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
). Then there exists a subcollection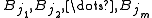
of these balls which are disjoint and satisfy
- where
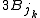denotes the ball with the same center as 
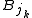but with three times the radius.
- Infinite version: Let
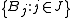be an arbitrary collection of balls in Rd (or, more generally, in a metric space) such that
- where
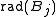denotes the radius of the ball Bj. Then there exists a subcollection
- of balls from the original collection which are disjoint and satisfy
Comments.
- The balls can have the form B = {y : d(y, c) < r} (an open ball with center c and radius r) or B = {y : d(y, c) ≤ r}. Then 3 B (or 5 B) denotes the ball of the same form, with 3 r (or 5 r) replacing r. Notice that the definition of balls requires r > 0.
- In the infinite version, the collection of balls can be countable or uncountable. The result may fail if the radii are not bounded: consider the family of all balls centered at 0 in Rd; any disjoint subfamily consists of only one ball B, and 5 B does not contain all the balls in this family.
Finite version
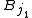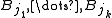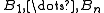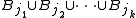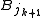With no loss of generality, we assume that the collection of balls is not empty; that is, n > 0. Let be the ball of largest radius. Inductively, assume that have been chosen. If there is some ball in that is disjoint from , let be such ball with maximal radius (breaking ties arbitrarily), otherwise, we set m := k and terminate the inductive definition.Now set
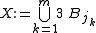. It remains to show that 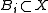for every 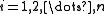. This is clear if 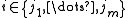. Otherwise, there necessarily is some 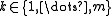such that Bi intersects 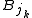and the radius of is at least as large as that of Bi. The triangle inequalityTriangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
then easily implies that
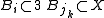, as needed. This completes the proof of the finite version.Infinite version
Let F denote the collection of all balls Bj, j ∈ J, that are given in the statement of the covering lemma. The following result provides a certain disjoint subcollection G of F. If this subcollection G is described as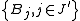, the property of G, stated below, readily proves that
Precised form of the covering lemma. Let F be a collection of (nondegenerate) balls in a metric space, with bounded radii. There exists a disjoint subcollection G of F with the following property:
-
- every ball B in F intersects a ball C in G such that B ⊂ 5 C.
(Degenerate balls only contain the center; they are excluded from this discussion.)
Let R be the supremum of the radii of balls in F. Consider the partition of F into subcollections Fn, n ≥ 0, consisting of balls B whose radius is in (2−n−1R, 2−nR]. A sequence Gn, with Gn ⊂ Fn, is defined inductively as follows. First, set H0 = F0 and let G0 be a maximal disjoint subcollection of H0. Assuming that G0,...,Gn have been selected, let
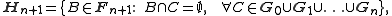
and let Gn+1 be a maximal disjoint subcollection of Hn+1. The subcollection
of F satisfies the requirements: G is a disjoint collection, and every ball B ∈ F intersects a ball C ∈ G such that B ⊂ 5 C.
Indeed, let n be such that B belongs to Fn. Either B does not belong to Hn, which implies n > 0 and means that B intersects a ball from the union of G0,...,Gn−1, or B ∈ Hn and by maximality of Gn, B intersects a ball in Gn. In any case, B intersects a ball C that belongs to the union of G0,...,Gn. Such a ball C has radius > 2−n−1R. Since the radius of B is ≤ 2−nR, it is less than twice that of C and the conclusion B ⊂ 5 C follows from the triangle inequality as in the finite version.
— Proof based on —
Remarks
- The constant 5 is not optimal. If the scale c−n, c > 1, is used instead of 2−n for defining Fn, the final value is 1 + 2c instead of 5. Any constant larger than 3 gives a correct statement of the lemma, but not 3.
- In the most general case of an arbitrary metric space, the selection of a maximal disjoint subcollection requires a form of Zorn's lemmaZorn's lemmaZorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
. - Using a finer analysis, when the original collection F is a Vitali covering of a subset E of Rd, one shows that the subcollection G, defined in the above proof, covers E up to a Lebesgue-negligible set (see below, "From the covering lemma to the covering theorem").
Applications and method of use
An application of the Vitali lemma is in proving the Hardy–Littlewood maximal inequality. As in this proof, the Vitali lemma is frequently used when we are, for instance, considering the d-dimensional Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
,
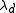, of a set E ⊂ Rd, which we know is contained in the union of a certain collection of balls 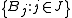, each of which has a measure we can more easily compute, or has a special property one would like to exploit. Hence, if we compute the measure of this union, we will have an upper bound on the measure of E. However, it is difficult to compute the measure of the union of all these balls if they overlap. By the Vitali lemma, we may choose a subcollection 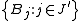which is disjoint and such that 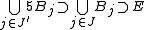. Therefore,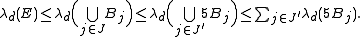Now, since increasing the radius of a d-dimensional ball by a factor of five increases its volume by a factor of 5d, we know that
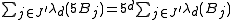
and thus
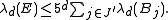
Vitali covering theorem
In the covering theorem, the aim is to cover, up to a "negligible set", a given set E ⊆ Rd by a disjoint subcollection extracted from a Vitali covering for E : a Vitali class or Vitali covering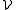 for E is a collection of sets such that, for every x ∈ E and δ > 0, there is a set U in the collection 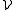such that x ∈ U and the diameterDiameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of U is non-zero and less than δ.
In the classical setting of Vitali, the negligible set is a Lebesgue negligible set, but measures other than the Lebesgue measure, and spaces other than Rd have also been considered, see below.
The following observation is useful: if
is a Vitali covering for E and if E is contained in an open set Ω ⊆ Rd, then the subcollection of sets U in 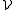that are contained in Ω is also a Vitali covering for E.Vitali's covering theorem for the Lebesgue measure
The next covering theorem for the Lebesgue measure λd is due to . A collection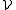 of measurable subsets of Rd is a regular family (in the sense of LebesgueHenri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
) if there exists a constant C such that
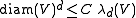
for every set V in the collection
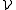.The family of cubes is an example of regular family
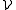, as is the family 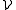(m) of rectangles in R2 such that the ratio of sides stays between m−1 and m, for some fixed m ≥ 1. If an arbitrary norm is given on Rd, the family of balls for the metric associated to the norm is another example. To the contrary, the family of all rectangles in R2 is not regular.Theorem. Let E ⊆ Rd be a measurable set with finite Lebesgue measure, and let
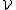be a regular family of closed subsets of Rd that is a Vitali covering for E. Then there exists a finite or countably infinite disjoint subcollection such that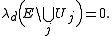The original result of is a special case of this theorem, in which d = 1 and
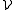is a collection of intervals that is a Vitali covering for a measurable subset E of the real line having finite measure.The theorem above remains true without assuming that E has finite measure. This is obtained by applying the covering result in the finite measure case, for every integer n ≥ 0, to the portion of E contained in the open annulus Ωn of points x such that n < |x| < n+1, see .
A somewhat related covering theorem is the Besicovitch covering theorem
Besicovitch covering theorem
In mathematical analysis, a Besicovitch cover, named after Abram Samoilovitch Besicovitch, is an open cover of a subset E of the Euclidean space RN by balls such that each point of E is the center of some ball in the cover....
. To each point a of a subset A ⊆ Rd, a Euclidean ball B(a, ra) with center a and positive radius ra is assigned. Then, as in the Vitali theorem, a subcollection of these balls is selected in order to cover A in a specific way. The main differences with the Vitali covering theorem are that on one hand, the disjointness requirement of Vitali is relaxed to the fact that the number Nx of the selected balls containing an arbitrary point x ∈ Rd is bounded by a constant Bd depending only upon the dimension d; on the other hand, the selected balls do cover the set A of all the given centers (for Vitali, a negligible error was allowed).
Vitali's covering theorem for the Hausdorff measure
One may have a similar objective when considering Hausdorff measureHausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
instead of Lebesgue measure. The theorem below applies in that case.
Theorem. Let Hs denote s-dimensional Hausdorff measure, let E ⊆ Rd be an Hs-measurable set and
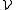a Vitali classof closed sets for E. Then there exists a (finite or countably infinite) disjoint subcollection
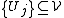such that either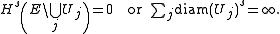Furthermore, if E has finite s-dimensional Hausdorff measure, then for any ε > 0, we may choose this subcollection {Uj} such that
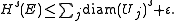
This theorem implies the result of Lebesgue given above. Indeed, when s = d, the Hausdorff measure Hs on Rd coincides with a multiple of the d-dimensional Lebesgue measure. If a disjoint collection
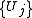is regular and contained in a measurable region B with finite Lebesgue measure, then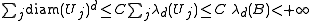which excludes the second possibility in the first assertion of the previous theorem. It follows that E is covered, up to a Lebesgue-negligible set, by the selected disjoint subcollection.
From the covering lemma to the covering theorem
The covering lemma can be used as intermediate step in the proof of the following basic form of the Vitali covering theorem. Actually, a little more is needed, namely the precised form of the covering lemma obtained in the "proof of the infinite version".- Theorem. For every subset E of Rd and every Vitali cover of E by a collection F of closed balls, there exists a disjoint subcollection G which covers E up to a Lebesgue-negligible set.
Without loss of generality, one can assume that all balls in F are nondegenerate and have radius ≤ 1. By the precised form of the covering lemma, there exists a disjoint subcollection G of F such that every ball B ∈ F intersects a ball C ∈ G for which B ⊂ 5 C. Let r > 0 be given, and let Z denote the set of points z ∈ E that are not contained in any ball from G and belong to the open ball B(r) of radius r, centered at 0. It is enough to show that Z is Lebesgue-negligible, for every given r.
Let G denote the subcollection of those balls in G that meet B(r). Consider the partition of G into sets Gn, n ≥ 0, consisting of balls that have radius in (2−n−1, 2−n]. Any ball B in F that meets B(r) is contained in B(r+2). It follows from the disjointness property of G that
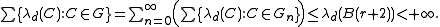
This implies that Gn is a finite set for every n. Given
ε > 0, we may select N such that
Let z ∈ Z be fixed. By definition of Z, this point z does not belong to the closed set K equal to the (finite) union of balls in Gk, k ≤ N. By the Vitali cover property, one can find a ball B ∈ F containing z, contained in B(r) and disjoint from K. By the property of G, the ball B meets C and is included in 5 C for some ball C ∈ G. One sees that C ∈ G because C intersects B(r), but C does not belong to any family Gk, k ≤ N, since B meets C but is disjoint from K. This proves that every point z ∈ Z is contained in the union of 5 C, when C varies in Gn, n > N, hence
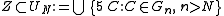
and
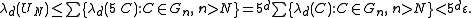
Since ε > 0 is arbitrary, this shows that Z is negligible.
Proof based on , with some notation from .
Infinite-dimensional spaces
The Vitali covering theorem is not valid in infinite-dimensional settings. The first result in this direction was given by David PreissDavid Preiss
David Preiss is a professor of mathematics at the University of Warwick and the winner of the 2008 LMS Pólya Prize for his 1987 result on Geometry of Measures, where he solved the remaining problem in the geometric theoretic structure of sets and measures in Euclidean space.David Preiss is...
in 1979: there exists a Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
γ on an (infinite-dimensional) separable Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H so that the Vitali covering theorem fails for (H, Borel(H), γ). This result was strengthened in 2003 by Jaroslav Tišer: the Vitali covering theorem in fact fails for every infinite-dimensional Gaussian measure on any (infinite-dimensional) separable Hilbert space.