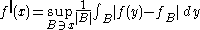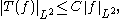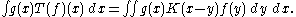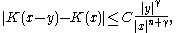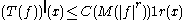Maximal function
Encyclopedia
Maximal functions appear in many forms in harmonic analysis
(an area of mathematics
). One of the most important of these is the Hardy–Littlewood maximal function. They play an important role in understanding, for example, the differentiability properties of functions, singular integrals and partial differential equations. They often provide a deeper and more simplified approach to understanding problems in these areas than other methods.
in the language of cricket
averages. Given a function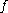 defined on
defined on 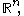 the uncentred Hardy–Littlewood maximal function
the uncentred Hardy–Littlewood maximal function 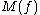 of
of 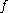 is defined as
is defined as
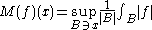
at each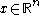 . Here, the supremum is taken over balls
. Here, the supremum is taken over balls 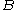 in
in 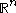 which contain the point
which contain the point  and
and 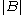 denotes the measure
denotes the measure
of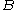 (in this case a multiple of the radius of the ball raised to the power
(in this case a multiple of the radius of the ball raised to the power  ). One can also study the centred maximal function, where the supremum is taken just over balls
). One can also study the centred maximal function, where the supremum is taken just over balls 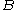 which have centre
which have centre  . In practice there is little difference between the two.
. In practice there is little difference between the two.
(a) For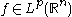 (
( ),
), 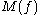 is finite almost everywhere.
is finite almost everywhere.
(b) If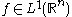 , then there exists a
, then there exists a  such that, for all
such that, for all 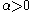 ,
,
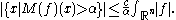
(c) If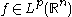 (
(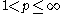 ), then
), then 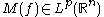 and
and
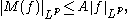
where depends only on
depends only on 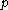 and
and  .
.
Properties (b) is called a weak-type bound of M(f). For an integrable function, it corresponds to the elementary Markov inequality; however, M(f) is never integrable, unless f is zero a.e., so that the proof of the weak bound (b) for M(f) requires a less elementary argument from geometric measure theory, such as the Vitali covering lemma
. Property (c) says the operator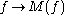 is bounded on
is bounded on 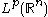 ; it is clearly true when
; it is clearly true when 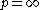 , since we cannot take an average of a bounded function and obtain a value larger than the largest value of the function. Property (c) for all other values of
, since we cannot take an average of a bounded function and obtain a value larger than the largest value of the function. Property (c) for all other values of  can then be deduced from these two facts by an interpolation argument.
can then be deduced from these two facts by an interpolation argument.
It is worth noting (c) does not hold for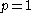 . This can be easily proved by calculating
. This can be easily proved by calculating 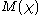 , where
, where 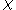 is the characteristic function of the unit ball centred at the origin.
is the characteristic function of the unit ball centred at the origin.
and Fatou's theorem
and in the theory of singular integral operators.
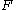 defined on the upper-half plane
defined on the upper-half plane 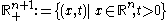 and produces a function
and produces a function 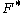 defined on
defined on  via the expression
via the expression
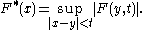
Obverse that for a fixed , the set
, the set 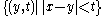 is a cone in
is a cone in 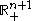 with vertex at
with vertex at  and axis perpendicular to the boundary of
and axis perpendicular to the boundary of 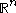 . Thus, the non-tangential maximal operator simply takes the supremum of the function
. Thus, the non-tangential maximal operator simply takes the supremum of the function 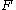 over a cone with vertex at the boundary of
over a cone with vertex at the boundary of 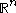 .
.
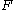 in which study of the non-tangential maximal function is important is formed from an approximation to the identity
in which study of the non-tangential maximal function is important is formed from an approximation to the identity
. That is, we fix an integrable smooth function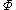 on
on 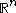 such that
such that 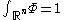 and set
and set
for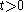 . Then define
. Then define
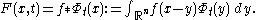
One can show that

and consequently obtain that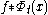 converges to
converges to 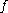 in
in  for all
for all 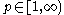 . Such a result can be used to show that the harmonic extension of an
. Such a result can be used to show that the harmonic extension of an 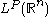 function to the upper-half plane converges non-tangentially to that function. More general results can be obtained where the Laplacian is replaced by an elliptic operator via similar techniques.
function to the upper-half plane converges non-tangentially to that function. More general results can be obtained where the Laplacian is replaced by an elliptic operator via similar techniques.
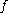 on
on 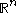 , the sharp maximal function
, the sharp maximal function 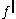 is defined as
is defined as
for each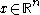 , where the supremum is taken over all balls
, where the supremum is taken over all balls 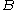 .
.
The sharp function can be used to obtain a point-wise inequality regarding singular integrals. Suppose we have an operator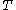 which is bounded on
which is bounded on 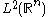 , so we have
, so we have
for all smooth and compactly supported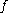 . Suppose also that we can realise
. Suppose also that we can realise 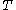 as convolution against a kernel
as convolution against a kernel 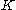 in the sense that, whenever
in the sense that, whenever 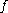 and
and 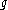 are smooth and have disjoint support
are smooth and have disjoint support
Finally we assume a size and smoothness condition on the kernel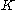 :
:
when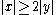 . Then for a fixed
. Then for a fixed  , we have
, we have
for all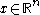 .
.
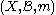 be a probability space, and
be a probability space, and 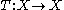 a measure-preserving endomorphism of
a measure-preserving endomorphism of 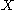 . The maximal function of a function
. The maximal function of a function 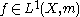 is
is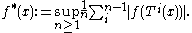
The maximal function of f verifies a weak bound analogous to the Hardy–Littlewood maximal inequality: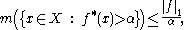
that is a restatement of the maximal ergodic theorem.
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
(an area of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
). One of the most important of these is the Hardy–Littlewood maximal function. They play an important role in understanding, for example, the differentiability properties of functions, singular integrals and partial differential equations. They often provide a deeper and more simplified approach to understanding problems in these areas than other methods.
The Hardy–Littlewood maximal function
In their original paper, G.H. Hardy and J.E. Littlewood explained their maximal inequalityin the language of cricket
Cricket
Cricket is a bat-and-ball game played between two teams of 11 players on an oval-shaped field, at the centre of which is a rectangular 22-yard long pitch. One team bats, trying to score as many runs as possible while the other team bowls and fields, trying to dismiss the batsmen and thus limit the...
averages. Given a function
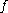 defined on
defined on 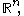 the uncentred Hardy–Littlewood maximal function
the uncentred Hardy–Littlewood maximal function 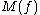 of
of 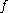 is defined as
is defined as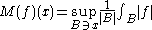
at each
 . Here, the supremum is taken over balls
. Here, the supremum is taken over balls  in
in  which contain the point
which contain the point  and
and 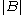 denotes the measure
denotes the measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of
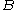 (in this case a multiple of the radius of the ball raised to the power
(in this case a multiple of the radius of the ball raised to the power  ). One can also study the centred maximal function, where the supremum is taken just over balls
). One can also study the centred maximal function, where the supremum is taken just over balls 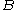 which have centre
which have centre  . In practice there is little difference between the two.
. In practice there is little difference between the two.Basic properties
The following statements are central to the utility of the Hardy–Littlewood maximal operator.(a) For
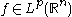 (
( ),
), 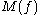 is finite almost everywhere.
is finite almost everywhere.(b) If
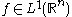 , then there exists a
, then there exists a  such that, for all
such that, for all 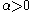 ,
,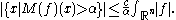
(c) If
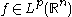 (
(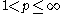 ), then
), then 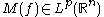 and
and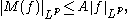
where
 depends only on
depends only on 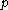 and
and  .
.Properties (b) is called a weak-type bound of M(f). For an integrable function, it corresponds to the elementary Markov inequality; however, M(f) is never integrable, unless f is zero a.e., so that the proof of the weak bound (b) for M(f) requires a less elementary argument from geometric measure theory, such as the Vitali covering lemma
Vitali covering lemma
In mathematics, the Vitali covering lemma is a combinatorial and geometric result commonly used in measure theory of Euclidean spaces. This lemma is an intermediate step, of independent interest, in the proof of the Vitali covering theorem. The covering theorem is credited to the Italian...
. Property (c) says the operator
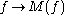 is bounded on
is bounded on 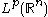 ; it is clearly true when
; it is clearly true when 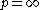 , since we cannot take an average of a bounded function and obtain a value larger than the largest value of the function. Property (c) for all other values of
, since we cannot take an average of a bounded function and obtain a value larger than the largest value of the function. Property (c) for all other values of  can then be deduced from these two facts by an interpolation argument.
can then be deduced from these two facts by an interpolation argument.It is worth noting (c) does not hold for
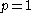 . This can be easily proved by calculating
. This can be easily proved by calculating 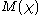 , where
, where 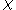 is the characteristic function of the unit ball centred at the origin.
is the characteristic function of the unit ball centred at the origin.Applications
The Hardy–Littlewood maximal operator appears in many places but some of its most notable uses are in the proofs of the Lebesgue differentiation theoremLebesgue differentiation theorem
In mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point...
and Fatou's theorem
Fatou's theorem
In complex analysis, Fatou's theorem, named after Pierre Fatou, is a statement concerning holomorphic functions on the unit disk and their pointwise extension to the boundary of the disk.-Motivation and statement of theorem:...
and in the theory of singular integral operators.
Non-tangential maximal functions
The non-tangential maximal function takes a function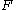 defined on the upper-half plane
defined on the upper-half plane 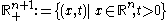 and produces a function
and produces a function 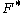 defined on
defined on  via the expression
via the expression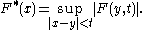
Obverse that for a fixed
 , the set
, the set 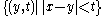 is a cone in
is a cone in 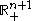 with vertex at
with vertex at  and axis perpendicular to the boundary of
and axis perpendicular to the boundary of 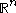 . Thus, the non-tangential maximal operator simply takes the supremum of the function
. Thus, the non-tangential maximal operator simply takes the supremum of the function 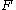 over a cone with vertex at the boundary of
over a cone with vertex at the boundary of 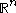 .
.Approximations of the identity
One particularly important form of functions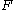 in which study of the non-tangential maximal function is important is formed from an approximation to the identity
in which study of the non-tangential maximal function is important is formed from an approximation to the identityApproximation to the identity
In mathematics, an approximation to the identity refers to a sequence or net that converges to the identity in some algebra. Specifically, it can mean:* Nascent delta function, most commonly* Mollifier, more narrowly* Approximate identity, more abstractly...
. That is, we fix an integrable smooth function
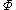 on
on 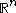 such that
such that 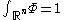 and set
and set
for
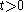 . Then define
. Then define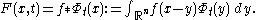
One can show that

and consequently obtain that
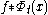 converges to
converges to 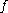 in
in  for all
for all 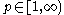 . Such a result can be used to show that the harmonic extension of an
. Such a result can be used to show that the harmonic extension of an 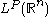 function to the upper-half plane converges non-tangentially to that function. More general results can be obtained where the Laplacian is replaced by an elliptic operator via similar techniques.
function to the upper-half plane converges non-tangentially to that function. More general results can be obtained where the Laplacian is replaced by an elliptic operator via similar techniques.The sharp maximal function
For a locally integrable function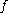 on
on 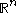 , the sharp maximal function
, the sharp maximal function 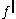 is defined as
is defined asfor each
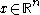 , where the supremum is taken over all balls
, where the supremum is taken over all balls 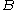 .
.The sharp function can be used to obtain a point-wise inequality regarding singular integrals. Suppose we have an operator
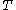 which is bounded on
which is bounded on 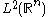 , so we have
, so we havefor all smooth and compactly supported
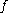 . Suppose also that we can realise
. Suppose also that we can realise 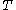 as convolution against a kernel
as convolution against a kernel 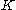 in the sense that, whenever
in the sense that, whenever 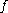 and
and 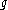 are smooth and have disjoint support
are smooth and have disjoint supportFinally we assume a size and smoothness condition on the kernel
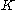 :
:when
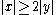 . Then for a fixed
. Then for a fixed  , we have
, we havefor all
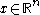 .
.Maximal functions in ergodic theory
Let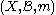 be a probability space, and
be a probability space, and 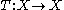 a measure-preserving endomorphism of
a measure-preserving endomorphism of 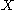 . The maximal function of a function
. The maximal function of a function 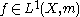 is
is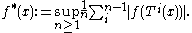
The maximal function of f verifies a weak bound analogous to the Hardy–Littlewood maximal inequality:
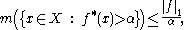
that is a restatement of the maximal ergodic theorem.