
Biorthogonal wavelet
Encyclopedia
A biorthogonal wavelet is a wavelet
where the associated wavelet transform
is invertible but not necessarily orthogonal
. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelet
s. One additional degree of freedom is the possibility to construct symmetric wavelet functions.
In the biorthogonal case, there are two scaling functions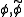 , which may generate different multiresolution analyses, and accordingly two different wavelet functions
, which may generate different multiresolution analyses, and accordingly two different wavelet functions 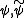 . So the numbers M and N of coefficients in the scaling sequences
. So the numbers M and N of coefficients in the scaling sequences 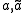 may differ. The scaling sequences must satisfy the following biorthogonality condition
may differ. The scaling sequences must satisfy the following biorthogonality condition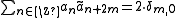 .
.
Then the wavelet sequences can be determined as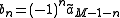 ,
, 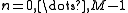 and
and 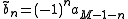 ,
, 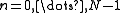 .
.
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
where the associated wavelet transform
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
is invertible but not necessarily orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelet
Orthogonal wavelet
An orthogonal wavelet is a wavelet where the associated wavelet transform is orthogonal.That is the inverse wavelet transform is the adjoint of the wavelet transform.If this condition is weakened you may end up with biorthogonal wavelets.- Basics :...
s. One additional degree of freedom is the possibility to construct symmetric wavelet functions.
In the biorthogonal case, there are two scaling functions
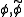 , which may generate different multiresolution analyses, and accordingly two different wavelet functions
, which may generate different multiresolution analyses, and accordingly two different wavelet functions 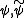 . So the numbers M and N of coefficients in the scaling sequences
. So the numbers M and N of coefficients in the scaling sequences 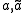 may differ. The scaling sequences must satisfy the following biorthogonality condition
may differ. The scaling sequences must satisfy the following biorthogonality condition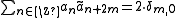 .
.Then the wavelet sequences can be determined as
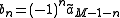 ,
, 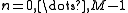 and
and 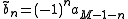 ,
, 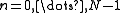 .
.

