Orthogonal wavelet
Encyclopedia
An orthogonal wavelet is a wavelet
where the associated wavelet transform
is orthogonal
.
That is the inverse wavelet transform is the adjoint of the wavelet transform.
If this condition is weakened you may end up with biorthogonal wavelet
s.
That is, it is a fractal
functional equation, called the refinement equation (twin-scale relation or dilation equation):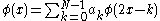
,
where the sequence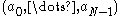
of real number
s is called a scaling sequence or scaling mask.
The wavelet proper is obtained by a similar linear combination,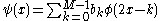
,
where the sequence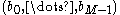
of real numbers is called a wavelet sequence or wavelet mask.
A necessary condition for the orthogonality of the wavelets is that the scaling sequence is orthogonal to any shifts of it by an even number of coefficients: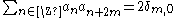
In this case there is the same number M=N of coefficients in the scaling as in the wavelet sequence, the wavelet sequence can be determined as
. In some cases the opposite sign is chosen.
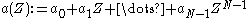(see Z-transform
). The maximally possible power A is called polynomial approximation order (or pol. app. power) or number of vanishing moments. It describes the ability to represent polynomials up to degree A-1 with linear combinations of integer translates of the scaling function.
In the biorthogonal case, an approximation order A of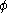
corresponds to A vanishing moments of the dual wavelet 
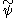, that is, the scalar products
of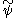
with any polynomial up to degree A-1 are zero. In the opposite direction, the approximation order à of 
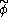is equivalent to à vanishing moments of 
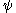. In the orthogonal case, A and à coincide.
A sufficient condition for the existence of a scaling function is the following: if one decomposes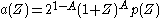
, and the estimate holds
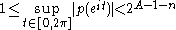for some 
,
holds, then the refinement equation has a n times continuously differentiable solution with compact support.
Examples:
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
where the associated wavelet transform
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
is orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
.
That is the inverse wavelet transform is the adjoint of the wavelet transform.
If this condition is weakened you may end up with biorthogonal wavelet
Biorthogonal wavelet
A biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets...
s.
Basics
The scaling function is a refinable function.That is, it is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
functional equation, called the refinement equation (twin-scale relation or dilation equation):
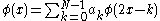,where the sequence
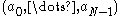of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is called a scaling sequence or scaling mask.
The wavelet proper is obtained by a similar linear combination,
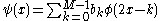,where the sequence
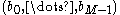of real numbers is called a wavelet sequence or wavelet mask.A necessary condition for the orthogonality of the wavelets is that the scaling sequence is orthogonal to any shifts of it by an even number of coefficients:
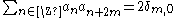
In this case there is the same number M=N of coefficients in the scaling as in the wavelet sequence, the wavelet sequence can be determined as
. In some cases the opposite sign is chosen.Vanishing moments, polynomial approximation and smoothness
A necessary condition for the existence of a solution to the refinement equation is that some power (1+Z)A, A>0, divides the polynomial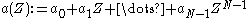 (see Z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
). The maximally possible power A is called polynomial approximation order (or pol. app. power) or number of vanishing moments. It describes the ability to represent polynomials up to degree A-1 with linear combinations of integer translates of the scaling function.
In the biorthogonal case, an approximation order A of
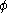corresponds to A vanishing moments of the dual wavelet 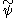, that is, the scalar productsDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of
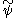with any polynomial up to degree A-1 are zero. In the opposite direction, the approximation order à of 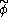is equivalent to à vanishing moments of 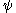. In the orthogonal case, A and à coincide.A sufficient condition for the existence of a scaling function is the following: if one decomposes
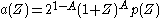, and the estimate holds 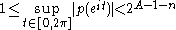for some ,holds, then the refinement equation has a n times continuously differentiable solution with compact support.
Examples:
, that is p(Z)=1, has n=A-2. The solutions are Schoenbergs B-splineB-splineIn the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
s of order A-1, where the (A-1)-th derivative is piecewise constant, thus the (A-2)-th derivative is Lipschitz-continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
. A=1 corresponds to the index function of the unit interval.- A=2 and p linear may be written as
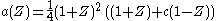. Expansion of this degree 3 polynomial and insertion of the 4 coefficients into the orthogonality condition results in c²=3. The positive root gives the scaling sequence of the D4-wavelet, see below.