
Refinable function
Encyclopedia
In mathematics
, in the area of wavelet
analysis, a refinable function is a function which fulfils some kind of self-similarity. A function is called refinable with respect to the mask
is called refinable with respect to the mask  if
if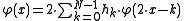
This condition is called refinement equation, dilation equation or two-scale equation.
Using the convolution
* of a function with a discrete mask and the dilation operator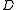 you can write more concisely:
you can write more concisely:
It means that you obtain the function, again, if you convolve the function with a discrete mask and then scale it back.
There is an obvious similarity to iterated function systems and de Rham curve
s.
The operator is linear.
is linear.
A refinable function is an eigenfunction
of that operator.
Its absolute value is not uniquely defined.
That is, if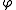 is a refinable function,
is a refinable function,
then for every the function
the function 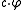 is refinable, too.
is refinable, too.
These functions play a fundamental role in wavelet
theory as scaling functions.
It may also be that there are several functions which are refinable with respect to the same mask.
If shall have finite support
shall have finite support
and the function values at integer arguments are wanted,
then the two scale equation becomes a system of simultaneous linear equations.
Let be the minimum index and
be the minimum index and 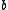 be the maximum index
be the maximum index
of non-zero elements of , then one obtains
, then one obtains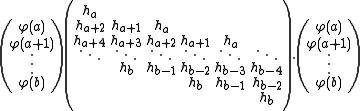 .
.
Using the discretization
operator, call it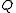 here, and the transfer matrix
here, and the transfer matrix
of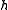 , named
, named 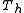 , this can be written concisely as
, this can be written concisely as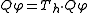 .
.
This is again a fixed-point equation
.
But this one can now be considered as an eigenvector-eigenvalue problem.
That is, a finitely supported refinable function exists only (but not necessarily),
if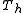 has the eigenvalue 1.
has the eigenvalue 1.
i.e. points of the form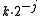 , with
, with  and
and 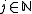 .
.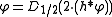
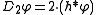

The star denotes the convolution
of a discrete filter with a function.
With this step you can compute the values at points of the form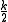 .
.
By replacing iteratedly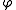 by
by 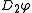 you get the values at all finer scales.
you get the values at all finer scales.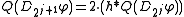
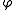 is refinable with respect to
is refinable with respect to  ,
,
and is refinable with respect to
is refinable with respect to 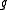 ,
,
then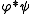 is refinable with respect to
is refinable with respect to 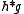 .
.
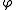 is refinable with respect to
is refinable with respect to 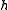 ,
,
and the derivative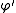 exists,
exists,
then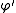 is refinable with respect to
is refinable with respect to 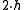 .
.
This can be interpreted as a special case of the convolution property,
where one of the convolution operands is a derivative of the Dirac impulse
.
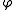 is refinable with respect to
is refinable with respect to 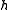 ,
,
and there is an antiderivative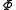 with
with
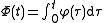 ,
,
then the antiderivative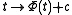
is refinable with respect to mask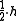
where the constant must fulfill
must fulfill
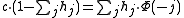 .
.
If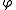 has bounded support,
has bounded support,
then we can interpret integration as convolution with the Heaviside function and apply the convolution law.
Let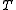 be the translation operator. It holds
be the translation operator. It holds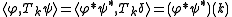
where is the adjoint of
is the adjoint of  with respect to convolution
with respect to convolution
,
i.e.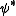 is the flipped and complex conjugate
is the flipped and complex conjugate
d version of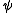 ,
,
i.e.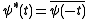 .
.
Because of the above property, is refinable with respect to
is refinable with respect to 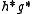 ,
,
and its values at integral arguments can be computed as eigenvectors of the transfer matrix.
This idea can be easily generalized to integrals of products of more than two refinable functions.
The design of continuous or smooth refinable functions is not obvious.
Before dealing with forcing smoothness it is necessary to measure smoothness of refinable functions.
Using the Villemoes machine
one can compute the smoothness of refinable functions in terms of Sobolev exponents
.
In a first step the refinement mask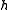 is divided into a filter
is divided into a filter 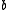 , which is a power of the smoothness factor
, which is a power of the smoothness factor 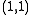 (this is a binomial mask) and a rest
(this is a binomial mask) and a rest 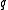 .
.
Roughly spoken, the binomial mask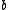 makes smoothness and
makes smoothness and
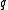 represents a fractal component, which reduces smoothness again.
represents a fractal component, which reduces smoothness again.
Now the Sobolev exponent is roughly
the order of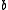 minus logarithm
minus logarithm
of the spectral radius
of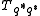 .
.
that is functions from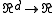 .
.
The most simple generalization is about tensor product
s.
If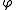 and
and 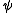 are refinable with respect to
are refinable with respect to 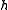 and
and 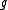 , respectively, then
, respectively, then 
is refinable with respect to .
.
The scheme can be generalized even more to different scaling factors with respect to different dimensions or even to mixing data between dimensions.
Instead of scaling by scalar factor like 2 the signal the coordinates are transformed by a matrix of integers.
of integers.
In order to let the scheme work, the absolute values of all eigenvalues of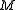 must be larger than one.
must be larger than one.
(Maybe it also suffices that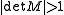 .)
.)
Formally the two-scale equation does not change very much: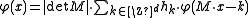
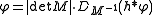
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
analysis, a refinable function is a function which fulfils some kind of self-similarity. A function
 is called refinable with respect to the mask
is called refinable with respect to the mask  if
if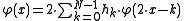
This condition is called refinement equation, dilation equation or two-scale equation.
Using the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
* of a function with a discrete mask and the dilation operator
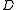 you can write more concisely:
you can write more concisely:
It means that you obtain the function, again, if you convolve the function with a discrete mask and then scale it back.
There is an obvious similarity to iterated function systems and de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
s.
The operator
 is linear.
is linear.A refinable function is an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of that operator.
Its absolute value is not uniquely defined.
That is, if
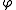 is a refinable function,
is a refinable function,then for every
 the function
the function 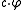 is refinable, too.
is refinable, too.These functions play a fundamental role in wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
theory as scaling functions.
Values at integral points
A refinable function is defined only implicitly.It may also be that there are several functions which are refinable with respect to the same mask.
If
 shall have finite support
shall have finite supportand the function values at integer arguments are wanted,
then the two scale equation becomes a system of simultaneous linear equations.
Let
 be the minimum index and
be the minimum index and 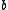 be the maximum index
be the maximum indexof non-zero elements of
 , then one obtains
, then one obtains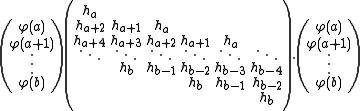 .
.Using the discretization
Ideal sampler
In signal processing, an ideal sampler is a theoretical operation whose input is a continuous signal and whose output is a sequence of instantaneous values of the signal at discrete moments of time, which is called a discrete signal....
operator, call it
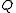 here, and the transfer matrix
here, and the transfer matrixTransfer matrix
The transfer matrix is a formulation in terms of a block-Toeplitz matrix of the two-scale equation, which characterizes refinable functions. Refinable functions play an important role in wavelet theory and finite element theory....
of
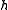 , named
, named 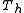 , this can be written concisely as
, this can be written concisely as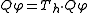 .
.This is again a fixed-point equation
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
But this one can now be considered as an eigenvector-eigenvalue problem.
That is, a finitely supported refinable function exists only (but not necessarily),
if
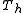 has the eigenvalue 1.
has the eigenvalue 1.Values at dyadic points
From the values at integral points you can derive the values at dyadic points,i.e. points of the form
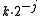 , with
, with  and
and 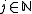 .
.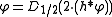
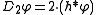

The star denotes the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of a discrete filter with a function.
With this step you can compute the values at points of the form
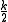 .
.By replacing iteratedly
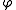 by
by 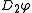 you get the values at all finer scales.
you get the values at all finer scales.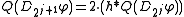
Convolution
If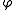 is refinable with respect to
is refinable with respect to  ,
,and
 is refinable with respect to
is refinable with respect to 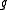 ,
,then
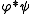 is refinable with respect to
is refinable with respect to 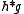 .
.Differentiation
If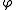 is refinable with respect to
is refinable with respect to 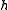 ,
,and the derivative
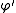 exists,
exists,then
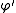 is refinable with respect to
is refinable with respect to 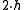 .
.This can be interpreted as a special case of the convolution property,
where one of the convolution operands is a derivative of the Dirac impulse
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
.
Integration
If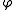 is refinable with respect to
is refinable with respect to 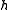 ,
,and there is an antiderivative
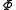 with
with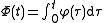 ,
,then the antiderivative
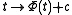
is refinable with respect to mask
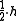
where the constant
 must fulfill
must fulfill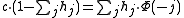 .
.If
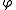 has bounded support,
has bounded support,then we can interpret integration as convolution with the Heaviside function and apply the convolution law.
Scalar products
Computing the scalar products of two refinable functions and their translates can be broken down to the two above properties.Let
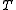 be the translation operator. It holds
be the translation operator. It holds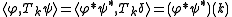
where
 is the adjoint of
is the adjoint of  with respect to convolution
with respect to convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
,
i.e.
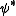 is the flipped and complex conjugate
is the flipped and complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
d version of
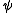 ,
,i.e.
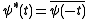 .
.Because of the above property,
 is refinable with respect to
is refinable with respect to 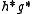 ,
,and its values at integral arguments can be computed as eigenvectors of the transfer matrix.
This idea can be easily generalized to integrals of products of more than two refinable functions.
Smoothness
A refinable function usually has a fractal shape.The design of continuous or smooth refinable functions is not obvious.
Before dealing with forcing smoothness it is necessary to measure smoothness of refinable functions.
Using the Villemoes machine
one can compute the smoothness of refinable functions in terms of Sobolev exponents
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
.
In a first step the refinement mask
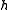 is divided into a filter
is divided into a filter 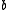 , which is a power of the smoothness factor
, which is a power of the smoothness factor 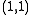 (this is a binomial mask) and a rest
(this is a binomial mask) and a rest 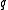 .
.Roughly spoken, the binomial mask
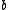 makes smoothness and
makes smoothness and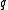 represents a fractal component, which reduces smoothness again.
represents a fractal component, which reduces smoothness again.Now the Sobolev exponent is roughly
the order of
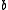 minus logarithm
minus logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of
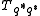 .
.Generalization
The concept of refinable functions can be generalized to functions of more than one variable,that is functions from
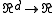 .
.The most simple generalization is about tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s.
If
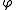 and
and 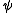 are refinable with respect to
are refinable with respect to 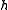 and
and 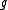 , respectively, then
, respectively, then 
is refinable with respect to
 .
.The scheme can be generalized even more to different scaling factors with respect to different dimensions or even to mixing data between dimensions.
Instead of scaling by scalar factor like 2 the signal the coordinates are transformed by a matrix
 of integers.
of integers.In order to let the scheme work, the absolute values of all eigenvalues of
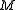 must be larger than one.
must be larger than one.(Maybe it also suffices that
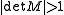 .)
.)Formally the two-scale equation does not change very much:
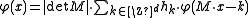
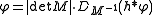
Examples
- If the definition is extended to distributionsDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, then the Dirac impulseDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
is refinable with respect to the unit vector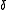 , that is known as Kronecker delta. The
, that is known as Kronecker delta. The  -th derivative of the Dirac distribution is refinable with respect to
-th derivative of the Dirac distribution is refinable with respect to  .
. - The Heaviside function is refinable with respect to
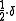 .
. - The truncated power functions with exponent
 are refinable with respect to
are refinable with respect to 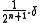 .
. - The triangular function is a refinable function. B-SplineB-splineIn the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
functions with successive integral nodes are refinable, because of the convolution theorem and the refinability of the characteristic function for the interval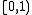 (a boxcar functionBoxcar functionIn mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...
(a boxcar functionBoxcar functionIn mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...
). - All polynomial functions are refinable. For every refinement mask there is a polynomial that is uniquely defined up to a constant factor. For every polynomial of degree
 there are many refinement masks that all differ by a mask of type
there are many refinement masks that all differ by a mask of type 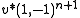 for any mask
for any mask  and the convolutional power
and the convolutional power 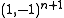 .
. - A rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
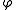 is refinable if and only if it can be represented using partial fractionPartial fractionIn algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
is refinable if and only if it can be represented using partial fractionPartial fractionIn algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
s as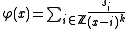 , where
, where 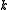 is a positivePositivePositive is a property of positivity and may refer to:- Mathematics and science :* Converging lens or positive lens, in optics* Plus sign, the sign "+" used to indicate a positive number* Positive , a polarity of electrical charge...
is a positivePositivePositive is a property of positivity and may refer to:- Mathematics and science :* Converging lens or positive lens, in optics* Plus sign, the sign "+" used to indicate a positive number* Positive , a polarity of electrical charge...
natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and is a real sequence with finitely many non-zero elements (a Laurent polynomial) such that
is a real sequence with finitely many non-zero elements (a Laurent polynomial) such that 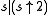 (read:
(read: 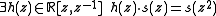 ). The Laurent polynomial
). The Laurent polynomial 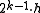 is the associated refinement mask.
is the associated refinement mask.

