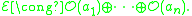Birkhoff-Grothendieck theorem
Encyclopedia
In mathematics, the Birkhoff–Grothendieck theorem classifies holomorphic vector bundle
s over the complex projective line
. In particular every holomorphic vector bundle over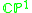
is a direct sum of holomorphic line bundle
s. The theorem was proved by , and is more or less equivalent to Birkhoff factorization
introduced by .
Every holomorphic vector bundle
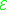on 
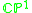is holomorphically isomorphic to a direct sum of line bundles:
The notation implies each summand is a Serre twist some number of times of the trivial bundle. The representation is unique up to permuting factors.
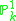for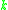 
any field.
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s over the complex projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. In particular every holomorphic vector bundle over
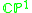is a direct sum of holomorphic line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s. The theorem was proved by , and is more or less equivalent to Birkhoff factorization
Birkhoff factorization
In mathematics, Birkhoff factorization or Birkhoff decomposition, introduced by , is the factorization of an invertible matrix M with coefficients that are Laurent polynomials in z into a product M = M+M0M−, where M+ has entries that are polynomials in z, M0 is diagonal, and...
introduced by .
Statement
More precisely, the statement of the theorem is as the following.Every holomorphic vector bundle
Holomorphic vector bundle
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map \pi:E\to X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the...
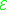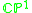on is holomorphically isomorphic to a direct sum of line bundles:
The notation implies each summand is a Serre twist some number of times of the trivial bundle. The representation is unique up to permuting factors.
Generalization
The same result holds in algebraic geometry for vector bundles ove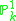r for 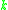any field.See also
- Algebraic geometry of projective spacesAlgebraic geometry of projective spacesProjective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...
- Euler exact sequence
- Splitting principleSplitting principleIn mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct...
- K-theoryK-theoryIn mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...