Blancmange curve
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
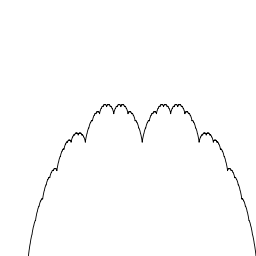
, the blancmange curve is a fractal curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi
Teiji Takagi
Teiji Takagi was a Japanese mathematician, best known for proving the Takagi existence theorem in class field theory....
who described it in 1903, or as the Takagi–Landsberg curve, a generalization of the curve. The name blancmange comes from its resemblance to a pudding of the same name
Blancmange
Blancmange is a sweet dessert commonly made with milk or cream and sugar thickened with gelatin, cornstarch or Irish moss, and often flavored with almonds. It is usually set in a mould and served cold. Although traditionally white, blancmanges are frequently given a pink color as well...
. It is a special case of the more general de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
.
The blancmange function is defined on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
by
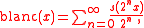
where
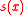is defined by 
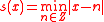,that is,
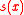is the distance from x to the nearest integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
The infinite sum defining
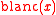converges absolutelyAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
for all x, but the resulting curve is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
. The blancmange function is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(indeed, uniformly continuous) but nowhere differentiable.
The Takagi–Landsberg curve is a slight generalization, given by
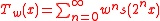
for a parameter w; thus the blancmange curve is the case
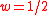. The value 
is known as the Hurst parameter. For 
, one obtains the parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
: the construction of the parabola by midpoint subdivision was described by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
.
The function can be extended to all of the real line: applying the definition given above shows that the function repeats on each unit interval.
Graphical construction
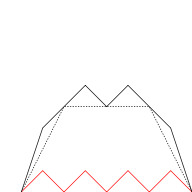
The blancmange curve can be visually built up out of sawtooth functions if the infinite sum is approximated by finite sums of the first few terms. In the illustration below, progressively finer sawtooth functions (shown in red) are added to the curve at each stage. |
 |
 |
 |
| n = 0 | n ≤ 1 | n ≤ 2 | n ≤ 3 |
Integrating the Blancmange curve
Given that the integral of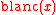
from 0 to 1 is 1/2, the identity 
allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required.-
Relation to simplicial complexes
Let-
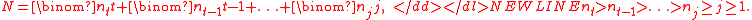
Define the Kruskal-Katona function
The Kruskal-Katona theorem states that this is the minimum number of (t-1)-simplexes that are faces of a set of N t-simplexes.
As t and N approach infinity,
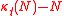(suitably normalized) approaches the blancmange curve.
External links
-