Blaschke product
Encyclopedia
In complex analysis
, the Blaschke product is a bounded analytic function
in the open unit disc constructed to have zeros at a (finite or infinite) sequence of prescribed complex number
s
inside the unit disc.
Blaschke products were introduced by . They are related to Hardy space
s.
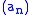inside the unit disk is said to satisfy the Blaschke condition when
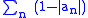
is convergent. Given a sequence obeying the Blaschke condition, the Blaschke product is defined as
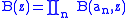
with factors
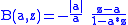
provided a ≠ 0. Here a* is the complex conjugate
of a. When a = 0 take B(0,z) = z.
The Blaschke product B(z) is analytic in the open unit disc, and is zero at the an only (with multiplicity
counted).
The sequence of an satisfying the convergence criterion above is sometimes called a Blaschke sequence.
states that if f is in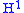
, the Hardy space
with integrable norm, and if f is not identically zero, then the zeroes of f (certainly countable in number) satisfy the Blaschke condition.
f can be extended to a continuous function on the closed unit disc
which maps the unit circle to itself. Then ƒ is equal to a finite Blaschke product
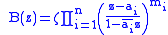
where ζ lies on the unit circle and mi is the multiplicity
of the zero ai, |ai| < 1. In particular, if ƒ satisfies the condition above and has no zeros inside the unit circle then ƒ is constant (this fact is also a consequence of the maximum principle
for harmonic function
s, applied to the harmonic function log(|ƒ(z)|)).
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the Blaschke product is a bounded analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in the open unit disc constructed to have zeros at a (finite or infinite) sequence of prescribed complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
- a0, a1, ...
inside the unit disc.
Blaschke products were introduced by . They are related to Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s.
Definition
A sequence of points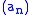 inside the unit disk is said to satisfy the Blaschke condition when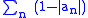is convergent. Given a sequence obeying the Blaschke condition, the Blaschke product is defined as
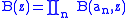
with factors
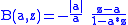
provided a ≠ 0. Here a* is the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of a. When a = 0 take B(0,z) = z.
The Blaschke product B(z) is analytic in the open unit disc, and is zero at the an only (with multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
counted).
The sequence of an satisfying the convergence criterion above is sometimes called a Blaschke sequence.
Szegő theorem
A theorem of Gábor SzegőGábor Szego
Gábor Szegő was a Hungarian mathematician. He was one of the foremost analysts of his generation and made fundamental contributions to the theory of Toeplitz matrices and orthogonal polynomials.-Life:...
states that if f is in
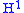, the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
with integrable norm, and if f is not identically zero, then the zeroes of f (certainly countable in number) satisfy the Blaschke condition.
Finite Blaschke products
Finite Blaschke products can be characterized (as analytic functions on the unit disc) in the following way: Assume that f is an analytic function on the open unit disc such thatf can be extended to a continuous function on the closed unit disc
which maps the unit circle to itself. Then ƒ is equal to a finite Blaschke product
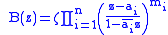
where ζ lies on the unit circle and mi is the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of the zero ai, |ai| < 1. In particular, if ƒ satisfies the condition above and has no zeros inside the unit circle then ƒ is constant (this fact is also a consequence of the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
for harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s, applied to the harmonic function log(|ƒ(z)|)).