
Bohlen-Pierce scale
Encyclopedia
The Bohlen–Pierce scale (BP scale) is a musical scale that offers an alternative to the octave
-repeating scales typical in Western
and other musics, specifically the diatonic scale
. Compared with octave-repeating scales, its interval
s are more consonant
with certain types of acoustic spectra
. It was independently described by Heinz Bohlen, Kees van Prooijen and John R. Pierce. Pierce, who, with Max Mathews
and others, published his discovery in 1984, renamed the Pierce 3579b scale and its chromatic variant the Bohlen–Pierce scale after learning of Bohlen's earlier publication. Bohlen had proposed the same scale based on consideration of the influence of combination tone
s on the Gestalt
impression of intervals and chords.
The intervals between BP scale pitch classes are based on odd integer
frequency
ratios, in contrast with the intervals in diatonic scales, which employ both odd and even ratios found in the harmonic series
. Specifically, the BP scale steps are based on ratios of integers whose factors are 3, 5, and 7. Thus the scale contains consonant harmonies based on the odd harmonic
overtones 3/5/7/9 . The chord formed by the ratio 3:5:7 serves much the same role as the 4:5:6 chord (a major triad ) does in diatonic scales (3:5:7 = 1:1.66:2.33 and 4:5:6 = 2:2.5:3 = 1:1.25:1.5).
The 3:5:7 chord may thus be considered the major triad of the BP scale. It is approximated by an interval of 6 equal-tempered BP semitone
s on bottom and an interval of 4 equal-tempered semitones on top (semitones: 0,6,10; ). A minor triad is thus 6 semitones on top and 4 semitones on bottom (0,4,10; ). 5:7:9 is the first inversion of the major triad (6,10,13; ).
A study of chromatic triads formed from arbitrary combinations of the 13 tones of the chromatic scale among twelve musicians and twelve untrained listeners found 0,1,2 (semitones) to be the most dissonant chord but 0,11,13 was considered the most consonant by the trained subjects and 0,7,10 was judged most consonant by the untrained subjects.
Every tone of the Pierce 3579b scale is in a major and minor triad except for tone II of the scale. There are thirteen possible keys. Modulation is possible through changing a single note, moving note II up one semitone causes the tonic to rise to what was note III (semitone: 3), which is considered the dominant
. VIII (semitone: 10) is considered the subdominant
.
). This interval is a perfect twelfth in diatonic
nomenclature (perfect fifth
when reduced by an octave), but as this terminology is based on step sizes and functions
not used in the BP scale, it is often called by a new name, tritave , in BP contexts, referring to its role as a pseudooctave, and using the prefix "tri-" (three) to distinguish it from the octave. In conventional scales, if a given pitch is part of the system, then all pitches one or more octaves higher or lower also are part of the system and, furthermore, are considered equivalent. In the BP scale, if a given pitch is present, then none of the pitches one or more octaves higher or lower are present, but all pitches one or more tritaves higher or lower are part of the system and are considered equivalent.
The BP scale's use of odd integer ratios is appropriate for timbres containing only odd harmonics. Because the clarinet
's spectrum (in the chalumeau
register) consists of primarily the odd harmonics, and the instrument overblows at the twelfth (or tritave) rather than the octave as most other woodwind instruments do, there is a natural affinity between it and the Bohlen–Pierce scale. In early 2006 clarinet maker Stephen Fox
began offering Bohlen–Pierce soprano clarinets for sale, and he produced the first BP tenor clarinet (six steps below the soprano) in 2010 and the first epsilon clarinet (four steps above the soprano) in 2011, while a contra clarinet (one tritave lower than the soprano) is under development.
!
| colspan="2" | C
| colspan="2" | D
| colspan="2" | E
| colspan="2" | F
| colspan="2" | G
| colspan="2" | H
| colspan="2" | J
| colspan="2" | A
| colspan="2" | B
| colspan="2" | C
|-
! Ratio
| colspan="2" | 1/1
| colspan="2" | 25/21
| colspan="2" | 9/7
| colspan="2" | 7/5
| colspan="2" | 5/3
| colspan="2" | 9/5
| colspan="2" | 15/7
| colspan="2" | 7/3
| colspan="2" | 25/9
| colspan="2" | 3/1
|-
! Step
|
| colspan="2" | T
| colspan="2" | s
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
|
|-
! Midi
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
|}>
A just BP scale may be constructed from four overlapping 3:5:7 chords, for example, V, II, VI, and IV, though different chords may be chosen to produce a similar scale:
(5/3) (7/5)
V IX III
|
III VII I
|
VI I IV
|
IV VIII II
and equal temperament
. The tempered
form, which divides the tritave into thirteen equal steps, has become the most popular form. Each step is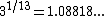 above the next, or about
above the next, or about 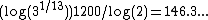 cents per step. The octave is divided into a fractional number of steps. Twelve equally tempered steps per octave are used in 12-tet
cents per step. The octave is divided into a fractional number of steps. Twelve equally tempered steps per octave are used in 12-tet
. The Bohlen–Pierce scale could be described as 8.202087-tet, because a full octave (1200 cents), divided by 146.3... cents per step, gives 8.202087 steps per octave.
Dividing the tritave into 13 equal steps tempers out, or reduces to a unison, both of the intervals 245/243 (about 14 cents, sometimes called the minor Bohlen–Pierce diesis
) and 3125/3087 (about 21 cents, sometimes called the major Bohlen–Pierce diesis) in the same way that dividing the octave into 12 equal steps reduces both 81/80 (syntonic comma
) and 128/125 (5-limit limma
) to a unison. A 7-limit linear temperament
tempers out both of these intervals; the resulting Bohlen–Pierce temperament no longer has anything to do with tritave equivalences or non-octave scales, beyond the fact that it is well adapted to using them. A tuning of 41 equal steps to the octave
(1200/41 = 29.27 cents per step) would be quite logical for this temperament. In such a tuning, a tempered perfect twelfth (1902.4 cents
, about a half cent larger than a just twelfth) is divided into 65 equal steps, resulting in a seeming paradox: Taking every fifth degree of this octave-based scale yields an excellent approximation to the non-octave-based equally tempered BP scale. Furthermore, an interval of five such steps generates (octave-based) MOS
es with 8, 9, or 17 notes, and the 8-note scale (comprising degrees 0, 5, 10, 15, 20, 25, 30, and 35 of the 41-equal scale) could be considered the octave-equivalent version of the Bohlen–Pierce scale.
Justly tuned
Equal-tempered
? Dave Benson suggests it helps to use only sounds with only odd harmonics, including clarinets or synthesized tones, but argues that because "some of the intervals sound a bit like intervals in [the more familiar] twelve-tone scale
, but badly out of tune," the average listener will continually feel "that something isn't quite right," due to social conditioning
.
Mathews and Pierce conclude that clear and memorable melodies may be composed in the BP scale, that "counterpoint sounds all right," and that "chordal passages sound like harmony," presumably meaning progression
, "but without any great tension or sense of resolution." In their 1989 study of consonance judgment, both intervals of the five chords rated most consonant by trained musicians are approximately diatonic intervals, suggesting that their training influenced their selection and that similar experience with the BP scale would similarly influence their choices.
Compositions using the Bohlen–Pierce scale include "Purity", the first movement of Curtis Roads
' Clang-Tint. Other computer composers to use the BP scale include Jon Appleton
, Richard Boulanger, Georg Hajdu
, and Juan Reyes' PPP.
(Hochschule für Musik und Theater Hamburg
) and the Boston Microtonal Society. Co-organizers were the Boston Goethe Institute, the Berklee College of Music
, the Northeastern University and the New England Conservatory of Music. The symposium participants, which included Heinz Bohlen, Max Mathews, Clarence Barlow, Curtis Roads
, David Wessel, Psyche Loui, Richard Boulanger, Georg Hajdu
, Paul Erlich
, Ron Sword, Julia Werntz, Larry Polansky, Manfred Stahnke, Stephen Fox, Elaine Walker, Todd Harrop, Gayle Young, Johannes Kretz, Arturo Grolimund, Kevin Foster, presented 20 papers on history and properties of the Bohlen–Pierce scale, performed more than 40 compositions in the novel system and introduced several new musical instruments.
s, and contains a complex network of harmonic relations due to the inclusion of coinciding harmonics of stacked 833 cent intervals. For example, "step 10 turns out to be identical with the octave (1200 cents) to the base tone, at the same time featuring the Golden Ratio
to step 3".
An expansion of the Bohlen–Pierce tritave from 13 equal steps to 39 equal steps, proposed by Paul Erlich, gives additional odd harmonics. The 13-step scale hits the odd harmonics 3/1; 5/3, 7/3; 7/5, 9/5; 9/7, and 15/7; while the 39-step scale includes all of those and many more (11/5, 13/5; 11/7, 13/7; 11/9, 13/9; 13/11, 15/11, 21/11, 25/11, 27/11; 15/13, 21/13, 25/13, 27/13, 33/13, and 35/13), while still missing almost all of the even harmonics (including 2/1; 3/2, 5/2; 4/3, 8/3; 6/5, 8/5; 9/8, 11/8, 13/8, and 15/8). The size of this scale is about 25 equal steps to a ratio slightly larger than an octave, so each of the 39 equal steps is slightly smaller than half of one of the 12 equal steps of the standard scale.
See also: Alpha scale
, Beta scale
, Delta scale
, Gamma scale
.
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
-repeating scales typical in Western
Classical music
Classical music is the art music produced in, or rooted in, the traditions of Western liturgical and secular music, encompassing a broad period from roughly the 11th century to present times...
and other musics, specifically the diatonic scale
Diatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
. Compared with octave-repeating scales, its interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
s are more consonant
Consonance
Consonance is a stylistic device, most commonly used in poetry and songs, characterized by the repetition of the same consonant two or more times in short succession, as in "pitter patter" or in "all mammals named Sam are clammy".Consonance should not be confused with assonance, which is the...
with certain types of acoustic spectra
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
. It was independently described by Heinz Bohlen, Kees van Prooijen and John R. Pierce. Pierce, who, with Max Mathews
Max Mathews
Max Vernon Mathews was a pioneer in the world of computer music.-Biography:...
and others, published his discovery in 1984, renamed the Pierce 3579b scale and its chromatic variant the Bohlen–Pierce scale after learning of Bohlen's earlier publication. Bohlen had proposed the same scale based on consideration of the influence of combination tone
Combination tone
A combination tone, also called a sum tone or a difference tone , can be any of at least three similar psychoacoustic phenomena. When two tones are played simultaneously, a listener can sometimes perceive an additional tone whose frequency is a sum or difference of the two frequencies...
s on the Gestalt
Gestalt psychology
Gestalt psychology or gestaltism is a theory of mind and brain of the Berlin School; the operational principle of gestalt psychology is that the brain is holistic, parallel, and analog, with self-organizing tendencies...
impression of intervals and chords.
The intervals between BP scale pitch classes are based on odd integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ratios, in contrast with the intervals in diatonic scales, which employ both odd and even ratios found in the harmonic series
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
. Specifically, the BP scale steps are based on ratios of integers whose factors are 3, 5, and 7. Thus the scale contains consonant harmonies based on the odd harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
overtones 3/5/7/9 . The chord formed by the ratio 3:5:7 serves much the same role as the 4:5:6 chord (a major triad ) does in diatonic scales (3:5:7 = 1:1.66:2.33 and 4:5:6 = 2:2.5:3 = 1:1.25:1.5).
Chords and modulation
3:5:7's intonation sensitivity pattern is similar to 4:5:6's (the just major chord), more similar than that of the minor chord. This similarity suggests that our ears will also perceive 3:5:7 as harmonic.The 3:5:7 chord may thus be considered the major triad of the BP scale. It is approximated by an interval of 6 equal-tempered BP semitone
Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s on bottom and an interval of 4 equal-tempered semitones on top (semitones: 0,6,10; ). A minor triad is thus 6 semitones on top and 4 semitones on bottom (0,4,10; ). 5:7:9 is the first inversion of the major triad (6,10,13; ).
A study of chromatic triads formed from arbitrary combinations of the 13 tones of the chromatic scale among twelve musicians and twelve untrained listeners found 0,1,2 (semitones) to be the most dissonant chord but 0,11,13 was considered the most consonant by the trained subjects and 0,7,10 was judged most consonant by the untrained subjects.
Every tone of the Pierce 3579b scale is in a major and minor triad except for tone II of the scale. There are thirteen possible keys. Modulation is possible through changing a single note, moving note II up one semitone causes the tonic to rise to what was note III (semitone: 3), which is considered the dominant
Dominant (music)
In music, the dominant is the fifth scale degree of the diatonic scale, called "dominant" because it is next in importance to the tonic,and a dominant chord is any chord built upon that pitch, using the notes of the same diatonic scale...
. VIII (semitone: 10) is considered the subdominant
Subdominant
In music, the subdominant is the technical name for the fourth tonal degree of the diatonic scale. It is so called because it is the same distance "below" the tonic as the dominant is above the tonic - in other words, the tonic is the dominant of the subdominant. It is also the note immediately...
.
Timbre and the tritave
3:1 serves as the fundamental harmonic ratio, replacing the diatonic scale's 2:1 (the octaveOctave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
). This interval is a perfect twelfth in diatonic
Diatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
nomenclature (perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
when reduced by an octave), but as this terminology is based on step sizes and functions
Diatonic function
In tonal music theory, a diatonic function is the specific, recognized role of each of the 7 notes and their chords in relation to the diatonic key...
not used in the BP scale, it is often called by a new name, tritave , in BP contexts, referring to its role as a pseudooctave, and using the prefix "tri-" (three) to distinguish it from the octave. In conventional scales, if a given pitch is part of the system, then all pitches one or more octaves higher or lower also are part of the system and, furthermore, are considered equivalent. In the BP scale, if a given pitch is present, then none of the pitches one or more octaves higher or lower are present, but all pitches one or more tritaves higher or lower are part of the system and are considered equivalent.
The BP scale's use of odd integer ratios is appropriate for timbres containing only odd harmonics. Because the clarinet
Clarinet
The clarinet is a musical instrument of woodwind type. The name derives from adding the suffix -et to the Italian word clarino , as the first clarinets had a strident tone similar to that of a trumpet. The instrument has an approximately cylindrical bore, and uses a single reed...
's spectrum (in the chalumeau
Chalumeau
This article is about the historical musical instrument. For the register on the clarinet that is named for this instrument, see Clarinet#Range....
register) consists of primarily the odd harmonics, and the instrument overblows at the twelfth (or tritave) rather than the octave as most other woodwind instruments do, there is a natural affinity between it and the Bohlen–Pierce scale. In early 2006 clarinet maker Stephen Fox
Stephen Fox (clarinet maker)
Stephen Fox is a clarinetist, saxophonist and clarinet maker based in Richmond Hill, Ontario, Canada. He is widely regarded as one of the world's foremost makers of custom, hand-built professional clarinets. Born in England, Fox completed a master's degree in physics at the University of...
began offering Bohlen–Pierce soprano clarinets for sale, and he produced the first BP tenor clarinet (six steps below the soprano) in 2010 and the first epsilon clarinet (four steps above the soprano) in 2011, while a contra clarinet (one tritave lower than the soprano) is under development.
Just tuning
A diatonic Bohlen–Pierce scale may be constructed with the following just ratios (chart shows the "Lambda" scale):| colspan="2" | C
| colspan="2" | D
| colspan="2" | E
| colspan="2" | F
| colspan="2" | G
| colspan="2" | H
| colspan="2" | J
| colspan="2" | A
| colspan="2" | B
| colspan="2" | C
|-
! Ratio
| colspan="2" | 1/1
| colspan="2" | 25/21
| colspan="2" | 9/7
Septimal major third
In music, the septimal major third , also called the supermajor third and sometimes Bohlen–Pierce third is the musical interval exactly or approximately equal to a just 9:7 ratio of frequencies, or alternately 14:11. It is equal to 435 cents, sharper than a just major third by the septimal...
| colspan="2" | 7/5
Tritone
In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones...
| colspan="2" | 5/3
Major sixth
In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two...
| colspan="2" | 9/5
Minor seventh
In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the...
| colspan="2" | 15/7
| colspan="2" | 7/3
Septimal minor third
In music, the septimal minor third , also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5...
| colspan="2" | 25/9
| colspan="2" | 3/1
|-
! Step
|
| colspan="2" | T
| colspan="2" | s
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
| colspan="2" | T
| colspan="2" | s
|
|-
! Midi
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
| colspan="2" |
|}>
A just BP scale may be constructed from four overlapping 3:5:7 chords, for example, V, II, VI, and IV, though different chords may be chosen to produce a similar scale:
(5/3) (7/5)
V IX III
|
III VII I
|
VI I IV
|
IV VIII II
Bohlen–Pierce temperament
Bohlen originally expressed the BP scale in both just intonationJust intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
and equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
. The tempered
Musical temperament
In musical tuning, a temperament is a system of tuning which slightly compromises the pure intervals of just intonation in order to meet other requirements of the system. Most instruments in modern Western music are tuned in the equal temperament system...
form, which divides the tritave into thirteen equal steps, has become the most popular form. Each step is
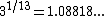 above the next, or about
above the next, or about 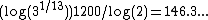 cents per step. The octave is divided into a fractional number of steps. Twelve equally tempered steps per octave are used in 12-tet
cents per step. The octave is divided into a fractional number of steps. Twelve equally tempered steps per octave are used in 12-tetEqual temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
. The Bohlen–Pierce scale could be described as 8.202087-tet, because a full octave (1200 cents), divided by 146.3... cents per step, gives 8.202087 steps per octave.
Dividing the tritave into 13 equal steps tempers out, or reduces to a unison, both of the intervals 245/243 (about 14 cents, sometimes called the minor Bohlen–Pierce diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
) and 3125/3087 (about 21 cents, sometimes called the major Bohlen–Pierce diesis) in the same way that dividing the octave into 12 equal steps reduces both 81/80 (syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
) and 128/125 (5-limit limma
Limma
The word limma or leimma can refer to several different musical intervals, whose only common property is their small size:*The original Pythagorean limma, 256/243, a Pythagorean interval ....
) to a unison. A 7-limit linear temperament
Regular temperament
Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios...
tempers out both of these intervals; the resulting Bohlen–Pierce temperament no longer has anything to do with tritave equivalences or non-octave scales, beyond the fact that it is well adapted to using them. A tuning of 41 equal steps to the octave
41 equal temperament
In music, 41 equal temperament, often abbreviated 41-tET, 41-EDO, or 41-ET, is the tempered scale derived by dividing the octave into 41 equally-sized steps . Each step represents a frequency ratio of 21/41, or 29.27 cents , an interval close in size to the septimal comma. 41-ET can be seen as a...
(1200/41 = 29.27 cents per step) would be quite logical for this temperament. In such a tuning, a tempered perfect twelfth (1902.4 cents
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
, about a half cent larger than a just twelfth) is divided into 65 equal steps, resulting in a seeming paradox: Taking every fifth degree of this octave-based scale yields an excellent approximation to the non-octave-based equally tempered BP scale. Furthermore, an interval of five such steps generates (octave-based) MOS
Generated collection
In diatonic set theory, a generated collection is a collection or scale formed by repeatedly adding a constant interval in integer notation, the generator, also known as an interval cycle, around the chromatic circle until a complete collection or scale is formed...
es with 8, 9, or 17 notes, and the 8-note scale (comprising degrees 0, 5, 10, 15, 20, 25, 30, and 35 of the 41-equal scale) could be considered the octave-equivalent version of the Bohlen–Pierce scale.
Intervals and scale diagrams
The following are the thirteen notes in the scale (cents rounded to nearest whole number):Justly tuned
| Interval (cents) | 133 | 169 | 133 | 148 | 154 | 147 | 134 | 147 | 154 | 148 | 133 | 169 | 133 | |||||||||||||||
| Note name | C | D♭ | D | E | F | G♭ | G | H | J♭ | J | A | B♭ | B | C | ||||||||||||||
| Note (cents) | 0 | 133 | 302 | 435 | 583 | 737 | 884 | 1018 | 1165 | 1319 | 1467 | 1600 | 1769 | 1902 | ||||||||||||||
Equal-tempered
| Interval (cents) | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | |||||||||||||||
| Note name | C | D♭ | D | E | F | G♭ | G | H | J♭ | J | A | B♭ | B | C | ||||||||||||||
| Note (cents) | 0 | 146 | 293 | 439 | 585 | 732 | 878 | 1024 | 1170 | 1317 | 1463 | 1609 | 1756 | 1902 | ||||||||||||||
| Steps | EQ interval | Cents in EQ | Just intonation interval | Traditional name | Cents in just intonation | Difference |
|---|---|---|---|---|---|---|
| 0 | 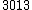 = 1.00 = 1.00 |
0.00 |  = 1.00 = 1.00 |
Unison | 0.00 | 0.00 |
| 1 | 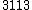 = 1.09 = 1.09 |
146.30 |  = 1.08 = 1.08 |
Great limma | 133.24 | 13.06 |
| 2 |  = 1.18 = 1.18 |
292.61 | 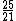 = 1.19 = 1.19 |
Quasi-tempered minor third | 301.85 | -9.24 |
| 3 | 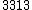 = 1.29 = 1.29 |
438.91 | 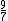 = 1.29 = 1.29 |
Septimal major third | 435.08 | 3.83 |
| 4 |  = 1.40 = 1.40 |
585.22 | 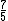 = 1.4 = 1.4 |
Lesser septimal tritone | 582.51 | 2.71 |
| 5 | 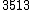 = 1.53 = 1.53 |
731.52 |  = 1.53 = 1.53 |
BP fifth | 736.93 | -5.41 |
| 6 | 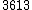 = 1.66 = 1.66 |
877.83 | 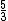 = 1.67 = 1.67 |
Just major sixth | 884.36 | -6.53 |
| 7 | 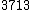 = 1.81 = 1.81 |
1024.13 | 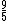 = 1.8 = 1.8 |
Greater just minor seventh | 1017.60 | 6.53 |
| 8 | 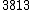 = 1.97 = 1.97 |
1170.44 | 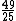 = 1.96 = 1.96 |
BP eighth | 1165.02 | 5.42 |
| 9 | 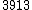 = 2.14 = 2.14 |
1316.74 | 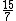 = 2.14 = 2.14 |
Septimal minor ninth | 1319.44 | -2.70 |
| 10 | 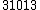 = 2.33 = 2.33 |
1463.05 | 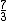 = 2.33 = 2.33 |
Septimal minimal tenth | 1466.87 | -3.82 |
| 11 | 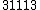 = 2.53 = 2.53 |
1609.35 | 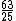 = 2.52 = 2.52 |
Quasi-tempered major tenth | 1600.11 | 9.24 |
| 12 | 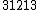 = 2.76 = 2.76 |
1755.66 | 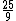 = 2.78 = 2.78 |
Classic augmented eleventh | 1768.72 | -13.06 |
| 13 | 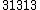 = 3.00 = 3.00 |
1901.96 | 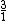 = 3.00 = 3.00 |
Just twelfth, "Tritave" | 1901.96 | 0.00 |
Music and composition
What does music using a Bohlen–Pierce scale sound like, aestheticallyAesthetics of music
Traditionally, the aesthetics of music or musical aesthetics concentrated on the quality and study of the beauty and enjoyment of music. The origin of this philosophic sub-discipline is sometimes attributed to Baumgarten in the 18th century, followed by Kant...
? Dave Benson suggests it helps to use only sounds with only odd harmonics, including clarinets or synthesized tones, but argues that because "some of the intervals sound a bit like intervals in [the more familiar] twelve-tone scale
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
, but badly out of tune," the average listener will continually feel "that something isn't quite right," due to social conditioning
Social conditioning
Social conditioning refers to the sociological process of training individuals in a society to act or respond in a manner generally approved by the society in general and peer groups within society. The concept is stronger than that of socialization, which refers to the process of inheriting norms,...
.
Mathews and Pierce conclude that clear and memorable melodies may be composed in the BP scale, that "counterpoint sounds all right," and that "chordal passages sound like harmony," presumably meaning progression
Chord progression
A chord progression is a series of musical chords, or chord changes that "aims for a definite goal" of establishing a tonality founded on a key, root or tonic chord. In other words, the succession of root relationships...
, "but without any great tension or sense of resolution." In their 1989 study of consonance judgment, both intervals of the five chords rated most consonant by trained musicians are approximately diatonic intervals, suggesting that their training influenced their selection and that similar experience with the BP scale would similarly influence their choices.
Compositions using the Bohlen–Pierce scale include "Purity", the first movement of Curtis Roads
Curtis Roads
Curtis Roads is a composer of electronic and electroacoustic music specializing in granular and pulsar synthesis, author, and computer programmer....
' Clang-Tint. Other computer composers to use the BP scale include Jon Appleton
Jon Appleton
Jon Howard Appleton is an American composer and teacher who was a pioneer in electro-acoustic music. His earliest compositions in the medium, e.g. Chef d'Oeuvre and Newark Airport Rock attracted attention because they established a new tradition some have called programmatic electronic music...
, Richard Boulanger, Georg Hajdu
Georg Hajdu
Georg Hajdu is a German composer of Hungarian descent. His work is dedicated to the combination of music, science and computer technology. He is noted for his opera Der Sprung – Beschreibung einer Oper and the network music performance environment Quintet.net.-Biography:Hajdu was born to Hungarian...
, and Juan Reyes' PPP.
Symposium
A first Bohlen–Pierce symposium took place in Boston on March 7 to 9, 2010, produced by composer Georg HajduGeorg Hajdu
Georg Hajdu is a German composer of Hungarian descent. His work is dedicated to the combination of music, science and computer technology. He is noted for his opera Der Sprung – Beschreibung einer Oper and the network music performance environment Quintet.net.-Biography:Hajdu was born to Hungarian...
(Hochschule für Musik und Theater Hamburg
Hochschule für Musik und Theater Hamburg
The Hochschule für Musik und Theater Hamburg is one of the larger universities of music in Germany.It was founded 1950 as Staatliche Hochschule für Musik on the base of the former private acting school of Annemarie Marks-Rocke and Eduard Marks.Studies include various music types from church music...
) and the Boston Microtonal Society. Co-organizers were the Boston Goethe Institute, the Berklee College of Music
Berklee College of Music
Berklee College of Music, located in Boston, Massachusetts, is the largest independent college of contemporary music in the world. Known primarily as a school for jazz, rock and popular music, it also offers college-level courses in a wide range of contemporary and historic styles, including hip...
, the Northeastern University and the New England Conservatory of Music. The symposium participants, which included Heinz Bohlen, Max Mathews, Clarence Barlow, Curtis Roads
Curtis Roads
Curtis Roads is a composer of electronic and electroacoustic music specializing in granular and pulsar synthesis, author, and computer programmer....
, David Wessel, Psyche Loui, Richard Boulanger, Georg Hajdu
Georg Hajdu
Georg Hajdu is a German composer of Hungarian descent. His work is dedicated to the combination of music, science and computer technology. He is noted for his opera Der Sprung – Beschreibung einer Oper and the network music performance environment Quintet.net.-Biography:Hajdu was born to Hungarian...
, Paul Erlich
Paul Erlich
Paul Erlich is a guitarist and music theorist living near Boston, Massachusetts. He is known for his seminal role in developing the theory of regular temperaments, including being the first to discover pajara temperament and its decatonic scales in 22-ET. He holds a Bachelor of Science degree in...
, Ron Sword, Julia Werntz, Larry Polansky, Manfred Stahnke, Stephen Fox, Elaine Walker, Todd Harrop, Gayle Young, Johannes Kretz, Arturo Grolimund, Kevin Foster, presented 20 papers on history and properties of the Bohlen–Pierce scale, performed more than 40 compositions in the novel system and introduced several new musical instruments.
Other unusual tunings or scales
Other non-octave tunings investigated by Bohlen include twelve steps in the tritave, named A12 by Enrique Moreno and based on the 4:7:10 chord , seven steps in the octave (7-tet) or similar 11 steps in the tritave, and eight steps in the octave, based on 5:7:9 and of which only the just version would be used. The Bohlen 833 cents scale is based on the Fibonacci sequence, although it was created from combination toneCombination tone
A combination tone, also called a sum tone or a difference tone , can be any of at least three similar psychoacoustic phenomena. When two tones are played simultaneously, a listener can sometimes perceive an additional tone whose frequency is a sum or difference of the two frequencies...
s, and contains a complex network of harmonic relations due to the inclusion of coinciding harmonics of stacked 833 cent intervals. For example, "step 10 turns out to be identical with the octave (1200 cents) to the base tone, at the same time featuring the Golden Ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
to step 3".
An expansion of the Bohlen–Pierce tritave from 13 equal steps to 39 equal steps, proposed by Paul Erlich, gives additional odd harmonics. The 13-step scale hits the odd harmonics 3/1; 5/3, 7/3; 7/5, 9/5; 9/7, and 15/7; while the 39-step scale includes all of those and many more (11/5, 13/5; 11/7, 13/7; 11/9, 13/9; 13/11, 15/11, 21/11, 25/11, 27/11; 15/13, 21/13, 25/13, 27/13, 33/13, and 35/13), while still missing almost all of the even harmonics (including 2/1; 3/2, 5/2; 4/3, 8/3; 6/5, 8/5; 9/8, 11/8, 13/8, and 15/8). The size of this scale is about 25 equal steps to a ratio slightly larger than an octave, so each of the 39 equal steps is slightly smaller than half of one of the 12 equal steps of the standard scale.
See also: Alpha scale
Alpha scale
The α scale is a non-octave-repeating musical scale which splits the minor third into two equal parts, or four equal parts of approximately 78 cents each . This totals approximately 15.39 steps per octave...
, Beta scale
Beta scale
The β scale is a non-octave-repeating musical scale which splits the perfect fourth into two equal parts, or eight equal parts of approximately 64 cents each . This totals approximately 18.75 steps per octave...
, Delta scale
Delta scale
The δ scale is a non-octave repeating musical scale. It may be regarded as the beta scale's reciprocal since it is, "as far 'down' the circle from α as β is 'up.'" As such it would split the minor second into eight equal parts of approximately 14 cents each...
, Gamma scale
Gamma scale
The γ scale is a non-octave repeating musical scale which splits the neutral third into two equal parts, or ten equal parts of 35 cents each...
.

